题目内容
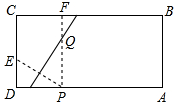
如图,四边形ABCD是平行四边形,连接AC.
(1)(4分)请根据以下语句画图,并标上相应的字母(用黑色字迹的钢笔或签字笔画).
①过点A画AE⊥BC于点E;
②过点C画CF∥AE,交AD于点F;
(2)(4分)在完成(1)后的图形中(不再添加其它线段和字母),请你找出一对全等三角形,并予以证明.
(1)(4分)请根据以下语句画图,并标上相应的字母(用黑色字迹的钢笔或签字笔画).
①过点A画AE⊥BC于点E;
②过点C画CF∥AE,交AD于点F;
(2)(4分)在完成(1)后的图形中(不再添加其它线段和字母),请你找出一对全等三角形,并予以证明.

(1)  (2)△ABC≌△CDA 。证明见解析
(2)△ABC≌△CDA 。证明见解析
 (2)△ABC≌△CDA 。证明见解析
(2)△ABC≌△CDA 。证明见解析(1)根据语句要求画图即可。
(2)首先根据平行四边形的性质和AE∥CF,可得①△ABC≌△CDA,②△AEC≌△CFA,③△ABE≌△CDF。
△ABC≌△CDA 。证明:∵ 四边形ABCD是平行四边形,∴ AB=CD,BC=DA。又∵ AC=CA,∴△ABC≌△CDA(SSS)。
下面给出其它两个的证明:
②△AEC≌△CFA。证明如下:
∵四边形ABCD是平行四边形,∴ AD∥BC。∴∠DAC=∠ACE。
∵AE∥CF,∴∠EAC=∠ACF。
∵AC=CA,∴△AEC≌△CFA(ASA)。
③△ABE≌△CDF。证明如下:
∵四边形ABCD是平行四边形,∴ AD∥BC,∠B=∠D,AB=CD 。
又∵AE∥CF,∴四边形AECF是平行四边形。
∴∠AEC=∠AFC。∴∠AEB=∠CFD。∴△ABE≌△CDF(AAS)。
(2)首先根据平行四边形的性质和AE∥CF,可得①△ABC≌△CDA,②△AEC≌△CFA,③△ABE≌△CDF。
△ABC≌△CDA 。证明:∵ 四边形ABCD是平行四边形,∴ AB=CD,BC=DA。又∵ AC=CA,∴△ABC≌△CDA(SSS)。
下面给出其它两个的证明:
②△AEC≌△CFA。证明如下:
∵四边形ABCD是平行四边形,∴ AD∥BC。∴∠DAC=∠ACE。
∵AE∥CF,∴∠EAC=∠ACF。
∵AC=CA,∴△AEC≌△CFA(ASA)。
③△ABE≌△CDF。证明如下:
∵四边形ABCD是平行四边形,∴ AD∥BC,∠B=∠D,AB=CD 。
又∵AE∥CF,∴四边形AECF是平行四边形。
∴∠AEC=∠AFC。∴∠AEB=∠CFD。∴△ABE≌△CDF(AAS)。

练习册系列答案
相关题目
 的四个顶点分别作对角线
的四个顶点分别作对角线 的平行线,所围成的四边形
的平行线,所围成的四边形 显然是平行四边形。在进一步学习时,小明和小亮产生了很大的意见分歧:
显然是平行四边形。在进一步学习时,小明和小亮产生了很大的意见分歧:

 中,点
中,点 分别在边AB、BC、CA上,且
分别在边AB、BC、CA上,且 ,
, .下
.下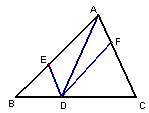
 是平行四边形
是平行四边形 ,那么四边形
,那么四边形 ,那么四边形
,那么四边形 且
且 ,那么四边形
,那么四边形