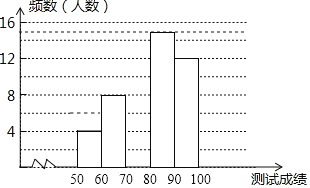
ĢāÄæÄŚČŻ
”¾ĢāÄæ”æ£Ø1£©ĪŹĢā·¢ĻÖ
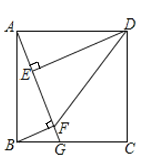
ČēĶ¼¢Ł£¬”÷ABCŗĶ”÷AED¶¼ŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬”ĻBAC=”ĻEAD=90”ć£¬µćBŌŚĻ߶ĪAEÉĻ£¬µćCŌŚĻ߶ĪADÉĻ£¬ĒėÖ±½ÓŠ“³öĻ߶ĪBEÓėĻ߶ĪCDµÄŹżĮæ¹ŲĻµ£ŗ £»
£Ø2£©²Ł×÷Ģ½¾æ
ČēĶ¼¢Ś£¬½«Ķ¼¢ŁÖŠµÄ”÷ABCČʵćAĖ³Ź±ÕėŠż×Ŗ£¬Šż×Ŗ½ĒĪŖ¦Į£Ø0”ć![]() ¦Į
¦Į![]() 360”ć£©£¬ĒėÅŠ¶Ļ²¢Ö¤Ć÷Ļ߶ĪBEÓėĻ߶ĪCDµÄŹżĮæ¹ŲĻµ£»
360”ć£©£¬ĒėÅŠ¶Ļ²¢Ö¤Ć÷Ļ߶ĪBEÓėĻ߶ĪCDµÄŹżĮæ¹ŲĻµ£»
£Ø3£©½ā¾öĪŹĢā
½«Ķ¼¢ŁÖŠµÄ”÷ABCČʵćAĖ³Ź±ÕėŠż×Ŗ£¬Šż×Ŗ½ĒĪŖ¦Į£Ø0”ć![]() ¦Į
¦Į![]() 360”ć£©£¬ČōDE=2AC£¬ŌŚŠż×ŖµÄ¹ż³ĢÖŠ£¬µ±ŅŌA”¢B”¢C”¢DĖĵćĪŖ¶„µćµÄĖıߊĪŹĒĘ½ŠŠĖıߊĪŹ±£¬ĒėÖ±½ÓŠ“³öŠż×Ŗ½Ē¦ĮµÄ¶ČŹż £®
360”ć£©£¬ČōDE=2AC£¬ŌŚŠż×ŖµÄ¹ż³ĢÖŠ£¬µ±ŅŌA”¢B”¢C”¢DĖĵćĪŖ¶„µćµÄĖıߊĪŹĒĘ½ŠŠĖıߊĪŹ±£¬ĒėÖ±½ÓŠ“³öŠż×Ŗ½Ē¦ĮµÄ¶ČŹż £®

”¾“š°ø”æ£Ø1£©![]() £»£Ø2£©
£»£Ø2£©![]() £¬Ö¤Ć÷¼ū½āĪö£»£Ø3£©45”ć£¬225”ć»ņ315”ć
£¬Ö¤Ć÷¼ū½āĪö£»£Ø3£©45”ć£¬225”ć»ņ315”ć
”¾½āĪö”æ
£Ø1£©øł¾ŻµČŃüÖ±½ĒČż½ĒŠĪµÄŠŌÖŹæɵĆAB£½AC£¬AE£½AD£¬ŌŁøł¾ŻµČĮæ¹ŲĻµæɵĆĻ߶ĪBEÓėĻ߶ĪCDµÄ¹ŲĻµ£»
£Ø2£©øł¾ŻµČŃüÖ±½ĒČż½ĒŠĪµÄŠŌÖŹæɵĆAB£½AC£¬AE£½AD£¬øł¾ŻŠż×ŖµÄŠŌÖŹæɵƔĻBAE£½”ĻCAD£¬øł¾ŻSASæÉÖ¤”÷BAE”Õ”÷CAD£¬øł¾ŻČ«µČČż½ĒŠĪµÄŠŌÖŹ¼“æÉĒó½ā£»
£Ø3£©øł¾ŻĘ½ŠŠĖıߊĪµÄŠŌÖŹæɵƔĻABC£½”ĻADC£½45”ć£¬ŌŁøł¾ŻµČŃüÖ±½ĒČż½ĒŠĪµÄŠŌÖŹ¼“æÉĒó½ā£®
½ā£ŗ£Ø1£©”ß”÷ABCŗĶ”÷AED¶¼ŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬”ĻBAC£½”ĻEAD£½90”ć£¬
”ąAB£½AC£¬AE£½AD£¬
”ąAEAB£½ADAC£¬
”ąBE£½CD£¬
¹Ź“š°øĪŖ£ŗBE£½CD£»
£Ø2£©”ß”÷ABCŗĶ”÷AED¶¼ŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬”ĻBAC£½”ĻEAD£½90”ć£¬
”ąAB£½AC£¬AE£½AD£¬
ÓÉŠż×ŖµÄŠŌÖŹµĆ£¬”ĻBAE£½”ĻCAD£¬
ŌŚ”÷BAEÓė”÷CADÖŠ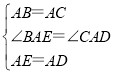 £¬
£¬
”ą”÷BAE”Õ”÷CAD£ØSAS£©
”ąBE£½CD£»
£Ø3£©ČēĶ¼£¬
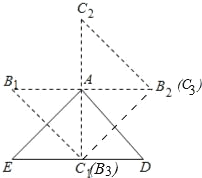
”ßŅŌA”¢B”¢C”¢DĖĵćĪŖ¶„µćµÄĖıߊĪŹĒĘ½ŠŠĖıߊĪ£¬”÷ABCŗĶ”÷AED¶¼ŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬
”ą”ĻABC£½”ĻADC£½45”ć£¬
”ßED£½2AC£¬
”ąAC£½CD£¬
”ą¢Łµ±CµćŠż×ŖÓŚC1Ī»ÖĆŹ±”ĻCAD£½45”ć£¬
¢Śµ±CµćŠż×ŖÓŚC2Ī»ÖĆŹ±”ĻCAD£½360”ć90”ć45”ć£½225”ć£¬
¢Ūµ±CµćŠż×ŖÓŚC3Ī»ÖĆŹ±”ĻCAD£½360”ć45”ć£½315”ć£¬
”ą½Ē¦ĮµÄ¶ČŹżŹĒ45”ć»ņ225”ć»ņ315”ć£¬
¹Ź“š°øĪŖ£ŗ45”ć»ņ225”ć»ņ315£®