题目内容
【题目】在“新冠”疫情期间,全国人民“众志成城,同心抗疫”,某商家决定将一个月获得的利润全部捐赠给社区用于抗疫.已知商家购进一批产品,成本为10元/件,拟采取线上和线下两种方式进行销售.调查发现,线下的月销量![]() (单位:件)与线下售价
(单位:件)与线下售价![]() (单位:元/件,
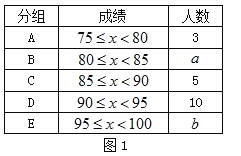
(单位:元/件,![]() )满足一次函数的关系,部分数据如下表:
)满足一次函数的关系,部分数据如下表:

(1)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)若线上售价始终比线下每件便宜2元,且线上的月销量固定为400件.试问:当![]() 为多少时,线上和线下月利润总和达到最大?并求出此时的最大利润.
为多少时,线上和线下月利润总和达到最大?并求出此时的最大利润.
【答案】(1)![]() ;(2)当线下售价定为19元/件时,月利润总和最大,此时最大利润是7300元.
;(2)当线下售价定为19元/件时,月利润总和最大,此时最大利润是7300元.
【解析】
(1)由待定系数法求出y与x的函数关系式即可;
(2)设线上和线下月利润总和为w元,则w=400(x-2-10)+y(x-10)=400x-4800+(-100x+2400)(x-10)=-100(x-19)2+7300,由二次函数的性质即可得出答案.
解:(1)因为y与x满足一次函数的关系,所以设y=kx+b.
将点(12,1200),(13,1100)代入函数解析式得![]()
解得![]()
∴![]() 与
与![]() 的函数关系式为
的函数关系式为![]() .
.
(2)设商家线上和线下的月利润总和为![]() 元,则可得
元,则可得
![]()
=400(x-12)+(-100x+2400)(x-10)
=-100x2+3800x-28800
=![]() ,
,
因为-100<0,
所以当x=19时,w有最大值,为7300,
所以当线下售价定为19元/件时,月利润总和最大,此时最大利润是7300元.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目