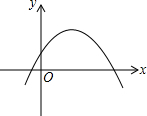题目内容
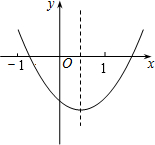
如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0),顶点坐标为(1,n),与y轴的交点在(0,2)、(0,3)之间(包含端点),则下列结论:
①当x>3时,y<0;
②3a+b>0;
③-1≤a≤-
;
④3≤n≤4中,
正确的是( )
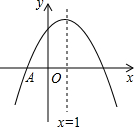
①当x>3时,y<0;
②3a+b>0;
③-1≤a≤-
| 2 |
| 3 |
④3≤n≤4中,
正确的是( )
| A.①② | B.③④ | C.①④ | D.①③ |
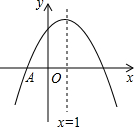
①∵抛物线y=ax2+bx+c与x轴交于点A(-1,0),对称轴直线是x=1,
∴该抛物线与x轴的另一个交点的坐标是(3,0),
∴根据图示知,当x>3时,y<0.
故①正确;
②根据图示知,抛物线开口方向向下,则a<0.
∵对称轴x=-
=1,
∴b=-2a,
∴3a+b=3a-2a=a<0,即3a+b<0.
故②错误;
③∵抛物线与x轴的两个交点坐标分别是(-1,0),(3,0),
∴-1×3=-3,
∴
=-3,则a=-
.
∵抛物线与y轴的交点在(0,2)、(0,3)之间(包含端点),
∴2≤c≤3,
∴-1≤-
≤-
,即-1≤a≤-
.
故③正确;
④根据题意知,a=-
,-
=1,
∴b=-2a=
,
∴n=a+b+c=
c.
∵2≤c≤3,
∴
≤
c≤4,即
≤n≤4.
故④错误.
综上所述,正确的说法有①③.
故选D.
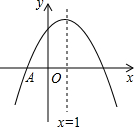
∴该抛物线与x轴的另一个交点的坐标是(3,0),
∴根据图示知,当x>3时,y<0.
故①正确;
②根据图示知,抛物线开口方向向下,则a<0.
∵对称轴x=-
| b |
| 2a |
∴b=-2a,
∴3a+b=3a-2a=a<0,即3a+b<0.
故②错误;
③∵抛物线与x轴的两个交点坐标分别是(-1,0),(3,0),
∴-1×3=-3,
∴
| c |
| a |
| c |
| 3 |
∵抛物线与y轴的交点在(0,2)、(0,3)之间(包含端点),
∴2≤c≤3,
∴-1≤-
| c |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
故③正确;
④根据题意知,a=-
| c |
| 3 |
| b |
| 2a |
∴b=-2a=
| 2c |
| 3 |
∴n=a+b+c=
| 4 |
| 3 |
∵2≤c≤3,
∴
| 8 |
| 3 |
| 4 |
| 3 |
| 8 |
| 3 |
故④错误.
综上所述,正确的说法有①③.
故选D.
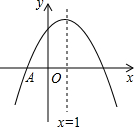

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目