题目内容
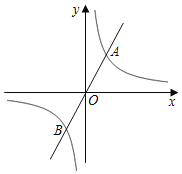
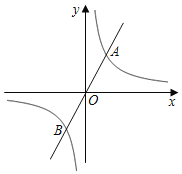
【题目】直线y=mx(m为常数)与双曲线y=![]() (k为常数)相交于A、B两点.
(k为常数)相交于A、B两点.
(1)若点A的横坐标为3,点B的纵坐标为﹣4.直接写出:k= ,m= ,mx>![]() 的解集为 .
的解集为 .
(2)若双曲线y=![]() (k为常数)的图象上有点C(x1,y1),D(x2,y2),当x1<x2时,比较y1与y2的大小.
(k为常数)的图象上有点C(x1,y1),D(x2,y2),当x1<x2时,比较y1与y2的大小.
【答案】(1)12,![]() ,﹣3<x<0或x>3;(2)y1<y2.
,﹣3<x<0或x>3;(2)y1<y2.
【解析】
(1)根据正比例函数与双曲线的交点关于原点对称得出A(3,4),B(-3,-4),进而得出k=3×4=12,m=![]() ,然后根据图象即可求得mx>
,然后根据图象即可求得mx>![]() 的解集;
的解集;
(2)根据反比例函数的性质即可判断.
解:(1)∵直线y=mx(m为常数)与双曲线y=![]() (k为常数)相交于A、B两点,点A的横坐标为3,点B的纵坐标为﹣4,
(k为常数)相交于A、B两点,点A的横坐标为3,点B的纵坐标为﹣4,
∴A(3,4),B(﹣3,﹣4),
∴k=3×4=12,m=![]() ,
,
由图象可知,mx>![]() 的解集为﹣3<x<0或x>3,
的解集为﹣3<x<0或x>3,
故答案为12,![]() ,﹣3<x<0或x>3;
,﹣3<x<0或x>3;
(2)若点C(x1,y1),D(x2,y2)在同一象限,即x1x2>0,y随x的增大而减小,
当x1<x2时,则y1>y2;
若点C(x1,y1),D(x2,y2)不在同一象限,即x1x2<0,
当x1<x2时,则点C(x1,y1)在第三象限,D(x2,y2)在第一象限,
则y1<y2.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目