题目内容
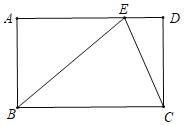
【题目】如图,在矩形ABCD中,点E在AD上,且BE=BC.
(1)EC平分∠BED吗?证明你的结论.
(2)若AB=1,∠ABE=45°,求BC的长.
【答案】(1)EC平分∠BED,证明见解析;(2)BC=![]() .
.
【解析】
(1)由矩形的性质得出∠DEC=∠ECB,由BE=BC得出∠ECB=∠BEC,即可得出∠DEC=∠BEC,结论得证;
(2)求出AE=AB=1,根据勾股定理求出BE即可.
解:(1)EC平分∠BED,证明如下:
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DEC=∠BCE,
∵BE=BC,
∴∠BEC=∠BCE,
∴∠BEC=∠DEC,
∴EC平分∠BED.
(2)∵四边形ABCD是矩形,
∴∠A=90°,
∵∠ABE=45°,
∴∠ABE=AEB=45°,
∴AE=AB=1,
由勾股定理得:![]() ,
,
∴BC=BE=![]() .
.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
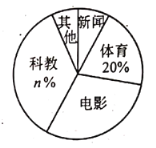
【题目】学校为了解全校![]() 名学生双休日在家最爱选择的电视频道情况,问卷要求每名学生从“新闻,体育,电影,科教,其他”五项中选择其一,随机抽取了部分学生,调查结果绘制成未完成的统计图表如下:
名学生双休日在家最爱选择的电视频道情况,问卷要求每名学生从“新闻,体育,电影,科教,其他”五项中选择其一,随机抽取了部分学生,调查结果绘制成未完成的统计图表如下:
频道 | 新闻 | 体育 | 电影 | 科教 | 其他 |
人数 |
|
|
|
|
|
![]() 求调查的学生人数及统计图表中
求调查的学生人数及统计图表中![]() 的值;
的值;
![]() 求选择其他频道在统计图中对应扇形的圆心角的度数;
求选择其他频道在统计图中对应扇形的圆心角的度数;
![]() 求全校最爱选择电影频道的学生人数.
求全校最爱选择电影频道的学生人数.
【题目】(阅读)x与代数式x2+2x﹣1的部分对应值如表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
x2+2x﹣1 | … | 2 | ﹣1 | ﹣2 | ﹣1 | 2 | … |
可知:当x=﹣3时,x2+2x﹣1=2>0,当x=﹣2时,x2+2x﹣1=﹣1<0,所以方程x2+2x﹣1=0的一个解在﹣3和﹣2之间.
(理解)(1)方程x2+2x﹣1=0的另一个解在两个连续整数 和 之间.
(应用)(2)若关于x的一元二次方程﹣x2+2x+m=0的一个解在1和2之间,求m的取值范围.