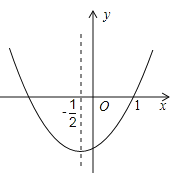ЬтФПФкШн
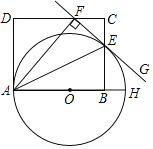
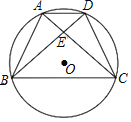
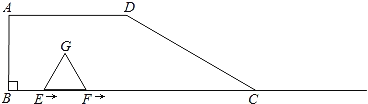
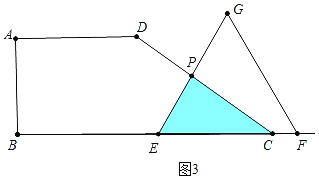
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDжаЃЌADЁЮBCЃЌЁЯBЃН90ЁуЃЌBCЃН6ЃЌADЃН3ЃЌЁЯDCBЃН30ЁуЃЌЕуEЁЂFЭЌЪБДгBЕуГіЗЂЃЌбиЩфЯпBCЯђгвдШЫйвЦЖЏЃЎвбжЊFЕувЦЖЏЫйЖШЪЧEЕувЦЖЏЫйЖШЕФ2БЖЃЌвдEFЮЊвЛБпдкCBЕФЩЯЗНзїЕШБпЁїEFGЃЎЩшEЕувЦЖЏОрРыЮЊxЃЈ0ЃМxЃМ6ЃЉЃЎ
ЃЈ1ЃЉЕуGдкЫФБпаЮABCDЕФБпЩЯЪБЃЌxЃНЁЁ ЁЁЃЛЕуFгыЕуCжиКЯЪБЃЌxЃНЁЁ ЁЁЃЛ
ЃЈ2ЃЉЧѓГіЪЙЁїDFCГЩЮЊЕШбќШ§НЧаЮЕФxЕФжЕЃЛ
ЃЈ3ЃЉЧѓЁїEFGгыЫФБпаЮABCDжиЕўВПЗжЕФУцЛ§yгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂжБНгаДГіyЕФзюДѓжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉ2ЃЛ3ЃЛЃЈ2ЃЉxЕФжЕЮЊ3Љ![]() Лђ3+
Лђ3+![]() Лђ2ЃЛ
Лђ2ЃЛ
ЃЈ3ЃЉ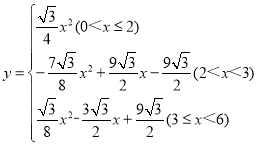 ЃЛ yЕФзюДѓжЕЮЊ
ЃЛ yЕФзюДѓжЕЮЊ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉШчЭМ1жаЃЌзїDHЁЭBCгкHЃЌдђЫФБпаЮABHDЪЧОиаЮЃЌЕБЕШБпШ§НЧаЮЁїEGFЕФИп=![]() ЪБЃЌЕуGдкADЩЯЃЌДЫЪБxЃН2ЃЌЕБЕуFгыCжиКЯЪБЃЌBEЃН
ЪБЃЌЕуGдкADЩЯЃЌДЫЪБxЃН2ЃЌЕБЕуFгыCжиКЯЪБЃЌBEЃН![]() BCЃН3МДПЩЃЛ
BCЃН3МДПЩЃЛ
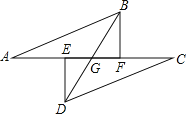
ЃЈ2ЃЉЗжШ§жжЧщПіЃКЂйЕБCFЃНCDЧвFдкCзѓВрЪБЃЌЂкЕБCFЃНCDЧвFдкCгвВрЪБЃЌЂлЕБFCЃНDFЪБЃЌЗжБ№ЙЙНЈЗНГЬМДПЩНтОіЮЪЬтЃЛ
ЃЈ3ЃЉЗжЭМ1ЃЌЭМ2ЃЌЭМ3Ш§жжЧщПіНтОіЮЪЬтЃКЂйЕБ0ЃМxЁм2ЪБЃЌШчЭМ1жаЃЌЁїEFGдкЫФБпаЮABCDФкВПЃЌжиЕўВПЗжОЭЪЧЁїEFGЃЛЂкЕБ2ЃМxЃМ3ЪБЃЌШчЭМ2жаЃЌЕуEЁЂFдкЯпЖЮBCЩЯЃЌЁїEFGгыЫФБпаЮABCDжиЕўВПЗжЮЊЫФБпаЮEFNMЃЛЂлЕБ3ЁмxЃМ6ЪБЃЌШчЭМ3жаЃЌЕуEдкЯпЖЮBCЩЯЃЌЕуFдкЩфЯпBCЩЯЃЌжиЕўВПЗжЪЧЁїECPЃЎ
НтЃКЃЈ1ЃЉШчЭМ1жаЃЌзїDHЁЭBCгкHЃЌдђЫФБпаЮABHDЪЧОиаЮЃЌ
ЁпADЃНBHЃН3ЃЌBCЃН6ЃЌ
ЁрCHЃНBCЉBHЃН3ЃЌ
дкRtЁїDHCжаЃЌCHЃН3ЃЌЁЯDCHЃН30ЁуЃЌ
ЁрDHЃНCHtan30ЁуЃН![]() ЃЌCD=2
ЃЌCD=2![]()
ЕБЕШБпШ§НЧаЮЁїEGFЕФИпЃН![]() ЪБЃЌЕуGдкADЩЯЃЌдђEF=2ЃЌгЩ2x-x=2ЃЌЕУxЃН2ЃЌ
ЪБЃЌЕуGдкADЩЯЃЌдђEF=2ЃЌгЩ2x-x=2ЃЌЕУxЃН2ЃЌ
ЕБЕуFгыCжиКЯЪБЃЌBE+EF=BC=6,Ыљ
вдBE=EF,дђBEЃН![]() BCЃН3ЃЌДЫЪБxЃН3ЃЌ
BCЃН3ЃЌДЫЪБxЃН3ЃЌ
ЫљвдЕуGдкЫФБпаЮABCDЕФБпЩЯЪБЃЌxЃН2ЃЌЕуFгыЕуCжиКЯЪБЃЌxЃН3ЃЌ
ЙЪД№АИЮЊ2ЃЛ3ЃЎ

ЃЈ2ЃЉзЂвтЕН0ЃМxЃМ6ЃЌЙЪЁїDFCЮЊЕШбќШ§НЧаЮжЛгаШ§жжЧщаЮЃК
ЂйЕБCFЃНCDЧвFдкCзѓВрЪБЃЌ6Љ2xЃН2![]() ЃЌЕУxЃН3Љ
ЃЌЕУxЃН3Љ![]() ЃЛ
ЃЛ
ЂкЕБCFЃНCDЧвFдкCгвВрЪБЃЌ2xЉ6ЃН2![]() ЃЌЕУxЃН3+
ЃЌЕУxЃН3+![]() ЃЛ
ЃЛ
ЂлЕБFCЃНDFЪБЃЌдкRtЁїFHDжаЃЌDF=![]() ЃЌЁр6Љ2xЃН2ЃЌЕУxЃН2ЃЛ
ЃЌЁр6Љ2xЃН2ЃЌЕУxЃН2ЃЛ
злЩЯЫљЪіЃЌxЕФжЕЮЊ3Љ![]() Лђ3+
Лђ3+![]() Лђ2ЃЛ
Лђ2ЃЛ
ЃЈ3ЃЉЂйЕБ0ЃМxЁм2ЪБЃЌШчЭМ1жаЃЌЁїEFGдкЫФБпаЮABCDФкВПЃЌЫљвдyЃН![]() x2ЃЌyЕФзюДѓжЕЮЊ
x2ЃЌyЕФзюДѓжЕЮЊ![]() ЃЌ
ЃЌ
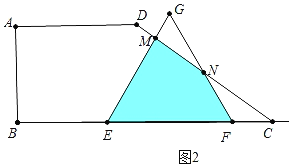
ЂкЕБ2ЃМxЃМ3ЪБЃЌШчЭМ2жаЃЌЕуEЁЂFдкЯпЖЮBCЩЯЃЌЁїEFGгыЫФБпаЮABCDжиЕўВПЗжЮЊЫФБпаЮEFNMЃЌ
ЁпЁЯFNCЃНЁЯFCNЃН30ЁуЃЌGF=EF= xЃЌ
ЁрFNЃНFCЃН6Љ2xЃЌ
ЁрGNЃН3xЉ6ЃЌ
ЁпЁЯGЃН60ЁуЃЌ
ЁрЁїGNMЪЧжБНЧШ§НЧаЮЃЌ
ЁрyЃНSЁїEFGЉSЁїGMNЃН![]() x2Љ
x2Љ![]() ЃЈ3xЉ6ЃЉ2ЃНЉ
ЃЈ3xЉ6ЃЉ2ЃНЉ![]() x2+
x2+![]() xЉ
xЉ![]() ЃЌyЕФзюДѓжЕЮЊ
ЃЌyЕФзюДѓжЕЮЊ![]() ЃЛ
ЃЛ
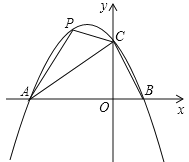
ЂлЕБ3ЁмxЃМ6ЪБЃЌШчЭМ3жаЃЌЕуEдкЯпЖЮBCЩЯЃЌЕуFдкЩфЯпBCЩЯЃЌжиЕўВПЗжЪЧЁїECPЃЌЧвЁЯECP+ЁЯCEP=90ЁуЃЌЁЯEPC=90ЁуЃЌЫљвдЁїECPЮЊжБНЧШ§НЧаЮЃЌEC=6-xЃЌдђ
yЃН![]() ЃЈ6ЉxЃЉ2ЃН
ЃЈ6ЉxЃЉ2ЃН![]() x2Љ
x2Љ![]() x+
x+![]() ЃЌyЕФзюДѓжЕЮЊ
ЃЌyЕФзюДѓжЕЮЊ![]() ЃЌ
ЃЌ
злЩЯЫљЪіЃЌyЕФзюДѓжЕЮЊ![]() ЃЌ
ЃЌ
ЙЪД№АИЮЊЃК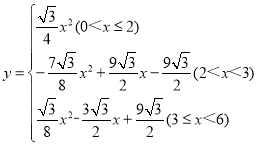 ЃЌyЕФзюДѓжЕЮЊ
ЃЌyЕФзюДѓжЕЮЊ![]() ЃЎ
ЃЎ

ЁОЬтФПЁПФЯФўКЃМЊаЧЫЎЙћХњЗЂЪаГЁРюДѓНуМвЕФЫЎЙћЕъЯњЪлШ§ЛЊРюЃЌИљОнЧАЖЮЪБМфЕФЯњЪлОбщЃЌУПЬьЕФЪлМл![]() ЃЈдЊ/ЯфЃЉгыЯњЪлСП
ЃЈдЊ/ЯфЃЉгыЯњЪлСП![]() ЃЈЯфЃЉгаШчБэЙиЯЕЃЌЧввбжЊ
ЃЈЯфЃЉгаШчБэЙиЯЕЃЌЧввбжЊ ![]() гы x жЎМфЕФКЏЪ§ЙиЯЕЪЧвЛДЮКЏЪ§ЃЎ
гы x жЎМфЕФКЏЪ§ЙиЯЕЪЧвЛДЮКЏЪ§ЃЎ
УПЯфЪлМлxЃЈдЊЃЉ | 68 | 67 | 66 | 65 | Ё | 40 |
УПЬьЯњСПyЃЈЯфЃЉ | 40 | 45 | 50 | 55 | Ё | 180 |
ЃЈ1ЃЉЧѓy гыxЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉШ§ЛЊРюЕФНјМлЪЧ 40 дЊ/ЯфЃЌШчЙћЩшУПЬьЛёЕУЕФгЏРћЮЊ ![]() дЊЃЌвЊЪЙИУЕъУПЬьЛёЕУзюДѓгЏРћЃЌдђУПЯфЪлМлЖрЩйдЊЃП
дЊЃЌвЊЪЙИУЕъУПЬьЛёЕУзюДѓгЏРћЃЌдђУПЯфЪлМлЖрЩйдЊЃП
ЃЈ3ЃЉ4 дТЗнЃЈАД 30 ЬьЫуЃЉСЌајвѕгъЃЌЯњЪлСПМѕЩйЃЎИУЕъОіЖЈВЩШЁНЕМлЯњЪлЃЌЙЪдкЃЈ2ЃЉЕФЬѕМўЯТЯњЪлСЫ 18 ЬьжЎКѓЃЌШ§ЛЊРюПЊЪМНЕМлЃЌЪлМлБШжЎЧАЯТНЕСЫ![]() ЃЌЭЌЪБШ§ЛЊРюЕФНјМлНЕЮЊ 29 дЊ/ЯфЃЌЯњЪлСПвВвђДЫБШдРДУПЬьЛёЕУзюДѓгЏРћЪБЩЯеЧСЫ
ЃЌЭЌЪБШ§ЛЊРюЕФНјМлНЕЮЊ 29 дЊ/ЯфЃЌЯњЪлСПвВвђДЫБШдРДУПЬьЛёЕУзюДѓгЏРћЪБЩЯеЧСЫ![]() ЃЌНЕМлЯњЪлСЫ 12 ЬьЕФШ§ЛЊРюЯњЪлзмгЏРћБШНЕМлЯњЪлЧАЕФЯњЪлзмгЏРћЩй 5670 дЊЃЌЧѓ
ЃЌНЕМлЯњЪлСЫ 12 ЬьЕФШ§ЛЊРюЯњЪлзмгЏРћБШНЕМлЯњЪлЧАЕФЯњЪлзмгЏРћЩй 5670 дЊЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ