Question

【题目】如图，AH是⊙O的直径，点E，F分别在矩形ABCD的边BC和CD上，B为直径OH上一点，AE平分∠FAH交⊙O于点E，过点E的直线FG⊥AF，垂足为F．

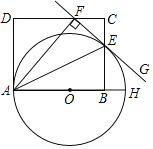
（1）求证：直线FG是⊙O的切线；

（2）若AD＝8，EB＝5，求⊙O的直径．

Answer 1

【答案】（1）见解析；（2）⊙O的直径为．

【解析】

（1）根据角平分线和半径相等，得∠OEA=∠EAF，推得OE∥AF，进而根据切线的判定即可证明；

（2）先证明Rt△ABE≌Rt△AFE，得AF=AB，再根据勾股定理即可求得半径的长，进而求得直径的长．

（1）如图，连接OE，

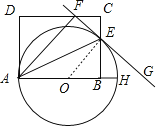
∵OA＝OE，

∴∠OAE＝∠OEA，

∵AE平分∠FAH，

∴∠OAE＝∠FAE，

∴∠OEA＝∠FAE，

∴OE∥AF，

∴∠AFE+∠OEF∠＝180°，

∵AF⊥GF，

∴∠AFE＝90°，

∴∠OEF＝90°，

∴OE⊥GF，

∵点E在圆上，OE是半径，

∴GF是⊙O的切线；

（2）设AB＝x，

∵四边形ABCD是矩形，

∴AB＝CD＝x，BC＝AD＝8，

∴CE＝BC﹣BE＝3，

∵AE是∠BAF的角平分线，BE⊥AB，EF⊥AF，

∴EF＝BE＝5，

在Rt△CEF中，根据勾股定理，得CF＝4，

∴DF＝CD﹣CF＝x﹣4，

AE＝AE，

∴Rt△ABE≌Rt△AFE（HL），

∴AF＝AB＝x，

在Rt△ADF中，x2﹣（x﹣4）2＝64，

∴x＝10，

∴AB＝10，

设⊙O的半径为r，

∴OB＝10﹣r，

在Rt△BOE中，r2＝（10﹣r）2+25，

∴r＝，

答：⊙O的直径为．