题目内容
【题目】已知二次函数![]() 的图象如图所示,对称轴为
的图象如图所示,对称轴为![]() .下列结论中,正确的是( )
.下列结论中,正确的是( )
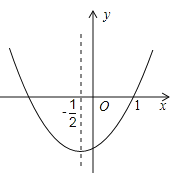
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
由二次函数的性质,即可确定a,b,c的符号,即可判定A是错误的;又由对称轴为![]() ,即可求得a=b,可判定B错误;由b>0,c<0,即可判定C错误;然后由抛物线与x轴交点坐标的特点,判定D正确.
,即可求得a=b,可判定B错误;由b>0,c<0,即可判定C错误;然后由抛物线与x轴交点坐标的特点,判定D正确.
∵开口向上,
∴a>0,
∵抛物线与y轴交于负半轴,
∴c<0,
∵对称轴在y轴左侧,
∴![]() ,
,
∴b>0,
∴abc<0,
故A选项错误;
B、∵对称轴:![]() ,
,
∴a=b,
∴![]() ,故B选项错误;
,故B选项错误;
C、∵b>0,c<0,
∴![]() ,
,
故C选项错误;
D、∵对称轴为![]() ,与x轴的一个交点的取值范围为x1>1,
,与x轴的一个交点的取值范围为x1>1,
∴与x轴的另一个交点的取值范围为x2<-2,
∴当x=-2时,4a-2b+c<0,
即4a+c<2b,
故D选项正确;
故答案为:D.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
【题目】为了帮助遭受自然灾害的地区,某学校号召同学们自愿捐款,已知第一次捐款总额为5800元,第二次捐款总额6000元,第二次捐款人数比第一次多20人,而且两次人均捐款额正好相等.
|
| |
每桶容积(升) | 20 | 15 |
每桶价格(元) | 5.6 | 4.5 |
(1)求两次各有多少人捐款?
(2)民政部门要求将捐款换成实物,统一运送到灾区.学校决定将捐款用于购买桶装水现有![]() 两种型号桶装水,上表是这两种桶装水的容积和单价.学校按民政局的救灾规划需订购总容积为40000升的桶装水,用同学们的捐款至少需订购
两种型号桶装水,上表是这两种桶装水的容积和单价.学校按民政局的救灾规划需订购总容积为40000升的桶装水,用同学们的捐款至少需订购![]() 型水多少桶.
型水多少桶.