题目内容
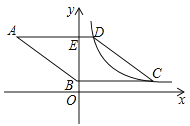
【题目】如图,在平面直角坐标系中,二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
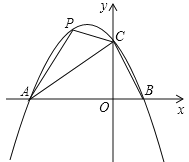
(1)求这个二次函数的解析式;
(2)点![]() 是直线
是直线![]() 上方的抛物线上一动点,是否存在点
上方的抛物线上一动点,是否存在点![]() ,使得
,使得![]() 的面积最大?若存在,求出点
的面积最大?若存在,求出点![]() 的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;
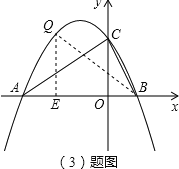
(3)点![]() 是直线
是直线![]() 上方的抛物线上一动点,过点
上方的抛物线上一动点,过点![]() 作
作![]() 轴于点
轴于点![]() .是否存在点
.是否存在点![]() ,使以点
,使以点![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,直接写出点
相似?若存在,直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
【答案】(1)![]() ;(2)存在,点
;(2)存在,点![]() ;(3)存在,
;(3)存在,![]() ,
,![]() .
.
【解析】
(1)把点A、B的坐标代入二次函数解析式,利用待定系数法求二次函数解析式解答;
(2)连接![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,设点
,设点![]() 的坐标为
的坐标为![]() ,得出
,得出![]() ,从而推出
,从而推出![]() ,即可推出当
,即可推出当![]() 时,
时,![]() 的面积最大,从而求出点
的面积最大,从而求出点![]() 的坐标.
的坐标.
(3)设点E的横坐标为c,表示出BE、QE,然后根据相似三角形对应边成比例,分OA和BE,OA和QE是对应边两种情况列出比例式求解即可.
(1)由抛物线![]() 过点
过点![]() ,
,![]() ,
,
则![]() ,解得
,解得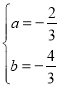 .
.
![]() 二次函数的解析式为
二次函数的解析式为![]() .
.
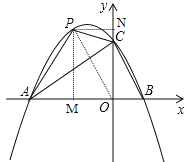
(2)存在.如图,连接![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() .
.
设点![]() 的坐标为
的坐标为![]() ,则
,则![]() .
.
![]() ,
,![]() ,
,![]() .
.
![]() 当
当![]() 时,
时,![]() ,
,
![]() .
.
![]()
![]()
![]()
![]() .
.
![]() ,
,
![]() 当
当![]() 时,
时,![]() 有最大值.
有最大值.
此时![]() .
.
![]() 存在点
存在点![]() ,使
,使![]() 的面积最大.
的面积最大.
(3)存在点![]() ,坐标为
,坐标为![]() ,
,![]() .
.
理由如下:设点E的横坐标为c,则点Q的坐标为![]() BE=1-c,
BE=1-c,
①OA和BE是对应边时,∵△BEQ∽△AOC,
∴![]() ,
,
即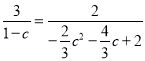 ,
,
整理得,c2+c-2=0,
解得c1=-2,c2=1(舍去),
此时,![]() ,
,
点Q(-2,2);
②OA和QE是对应边时,∵△QEB∽△AOC,
∴![]() ,
,
即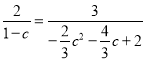 ,
,
整理得,4c2-c-3=0,
解得![]() ,c2=1(舍去),
,c2=1(舍去),
此时,![]() ,
,
点![]() ;
;
综上所述,存在点![]() ,
,![]() 使以点B、Q、E为顶点的三角形与△AOC相似.
使以点B、Q、E为顶点的三角形与△AOC相似.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目