题目内容
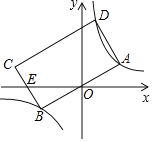
【题目】已知:如图点A,E,F,C在同一直线上,AE=EF=FC,过E,F分别作DE⊥AC,BF⊥AC,连结AB,CD,BD,BD交AC于点G,若AB=CD.
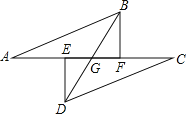
(1)求证:△ABF≌△CDE.
(2)若AE=ED=2,求BD的长.
【答案】(1)见解析;(2)BD=2![]() .
.
【解析】
(1)利用HL定理证明△ABF≌△CDE;
(2)证明△DEG≌△BFG,根据全等三角形的性质得到EG=FG=![]() EF=1,DG=BG,根据勾股定理计算,得到答案.
EF=1,DG=BG,根据勾股定理计算,得到答案.
(1)证明:∵AE=EF=FC,
∴AF=CE,
在Rt△AFB和Rt△CED中,
![]() ,
,
∴Rt△AFB≌Rt△CED(HL);
(2)解:∵△AFB≌△CED,
∴DE=BF,
在△DEG和△BFG中,
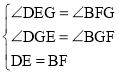 ,
,
∴△DEG≌△BFG(AAS)
∴EG=FG=![]() EF=1,DG=BG,
EF=1,DG=BG,
由勾股定理得,DG=![]() =
=![]() ,
,
∴BD=2DG=2![]() .
.

【题目】某数学老师为了了解学生在数学学习中常见错误的纠正情况,收集整理了学生在作业和考试中的常见错误,编制了10道选择题,每题3分,对他所教的初三(1)班、(2)班进行了检测,如图表示从两班各随机抽取的10名学生的得分情况.
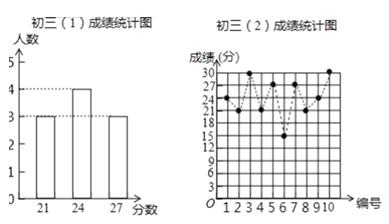
(1)利用图中提供的信息,补全下表:
班级 | 平均数/分 | 中位数/分 | 众数/分 | 方差/分 |
初三(1)班 | 24 | 24 | ________ | 5.4 |
初三(2)班 | 24 | _________ | 21 | ________ |
(2)哪个班的学生纠错的得分更稳定?若把24分以上(含24分)记为“优秀”,两班各40名学生,请估计两班各有多少名学生成绩优秀;
(3)现从两个班抽取了数学成绩最好的甲、乙、丙、丁四位同学,并随机分成两组进行数学竞赛,求恰好选中甲、乙一组的概率.
【题目】某校团委举办了一次“中国梦,我的梦”演讲比赛,满分10分,学生得分均为整数,成绩达6分以上(含6分)为合格,达9分以上(含9分)为优秀.这次竞赛中甲,乙两组学生成绩分布的条形统计图如下:
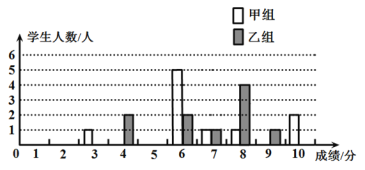
(1)将下表补充完整:
组别 | 平均分 | 中位数 | 众数 | 方差 | 合格率 | 优秀率 |
甲 | 6.8 |
| 6 | 3.96 | 90% | 20% |
乙 |
| 7.5 |
| 2.76 | 80% | 10% |
(2)小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上表可知,小明是 组学生(填“甲””或“乙”);
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你给出两条支持乙组同学观点的理由.