题目内容
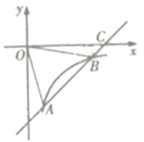
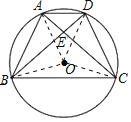
【题目】如图,⊙O是四边形ABCD的外接圆,对角线AC与BD相交于点E,且AE=DE,连接AD、CB.
(1)求证:AB=CD;
(2)在不添加任何辅助线的情况下,直接写出图中所有的全等三角形.
【答案】(1)详见解析;(2)详见解析
【解析】
(1)根据圆周角定理得到:∠AOB=∠DOC,则由圆心角、弧,弦的关系证得结论;
(2)根据全等三角形的判定定理解答.
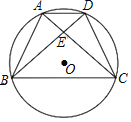
(1)证明:如图,连接OA、OB、OC、OD,
∵AE=DE,
∴∠ADB=∠DAC,
∴∠AOB=∠DOC,
∴AB=CD;
(2)解:①在△ABD与△DCA中,
 .
.
故△ABD≌△DCA(AAS);
②在△ABE与△DCE中,
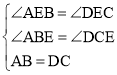 .
.
故△ABE≌△DCE(AAS);
③由AB=DC知,∠ACB=∠DBC.
在△ABC与△DCB中,
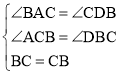 .
.
故△ABC≌△DCB(AAS).

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目