题目内容
【题目】如图,在平面直角坐标系中,把抛物线![]() 先向右平移1个单位长度,再向下平移4个单位长度,得到抛物线
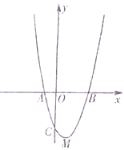
先向右平移1个单位长度,再向下平移4个单位长度,得到抛物线![]() ,所得抛物线与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,顶点为M.
,所得抛物线与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,顶点为M.
(1)写出h、k的值及点A、B的坐标;
(2)判断![]() 的形状,并计算其面积;
的形状,并计算其面积;
(3)点P是抛物线上的一动点,在y轴上存在点Q,使以点A、B、P、Q为顶点组成的四边形是平行四边形,求点P的坐标.
【答案】(1)![]() ,
,![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() 是直角三角形,
是直角三角形,![]() ;(3)点P的坐标为(4,5),(-4,21)或(2,-3)
;(3)点P的坐标为(4,5),(-4,21)或(2,-3)
【解析】
(1)根据左加右减,上加下减的方法求出函数解析式为![]() ,可得h、k的值,解方程
,可得h、k的值,解方程![]() 可求出点A、B的坐标;
可求出点A、B的坐标;
(2)首先求得点C和点M的坐标,然后求得BC、CM及BM的长,最后利用勾股定理逆定理判定直角三角形即可;
(3)分两AB为边和AB为对角线两种情况讨论计算即可.
(1)∵抛物线y=x2先向右平移1个单位,再向下平移4个单位,得到抛物线y=(x1)24,
∴h=1,k=4;
令y=0,即(x1)24=0
解得x=1或x=3,
∴A(1,0),B(3,0);
(2)![]() 令
令![]() ,得
,得![]() ,
,
![]() 点C的坐标为(0,-3),点M的坐标为(1,-4),
点C的坐标为(0,-3),点M的坐标为(1,-4),
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() 是直角三角形,
是直角三角形,
![]() ;
;
(3)由(1)知,抛物线![]() ,
,
![]()
![]() 设
设![]() ,
,
![]() ,
,![]() ,
,![]() ,AB的中点N(1,0),
,AB的中点N(1,0),
![]() 以点A、B、P、Q为顶点组成的四边形是平行四边形,
以点A、B、P、Q为顶点组成的四边形是平行四边形,
![]() 分以下情况.
分以下情况.
①当AB为边时,![]() ,
,![]() ,
,
![]() 或-4,当
或-4,当![]() 时,
时,![]() ,
,
![]() ;
;
当![]() 时,
时,![]() ,
,
![]() ;
;
②当AB为对角线时,点N是PQ的中点,
![]() ,
,![]() ,
,![]() ,
,
![]() 点P的坐标为(4,5),(-4,21)或(2,-3).
点P的坐标为(4,5),(-4,21)或(2,-3).

 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案【题目】“重整行装再出发,驰而不息再争创”,2018年5月8日兰州市召开了新一轮全国文明城市创建启动大会.某校为了更好地贯彻落实创建全国文明城市目标,举办了“我是创城小主人”的知识竞赛.该校七年级、八年级分别有300人,现从中各随机抽取10名同学的测试成绩进行调查分析,成绩如下:
七年级 | 85 | 65 | 84 | 78 | 100 | 78 | 85 | 85 | 98 | 83 |
八年级 | 96 | 60 | 87 | 78 | 87 | 87 | 89 | 100 | 83 | 96 |
整理、描述数据:
分数段 |
|
|
|
|
七年级人数 | 1 | 2 | 5 | 2 |
八年级人数 | 1 | 1 | 5 | 3 |
分析数据:
年级 | 平均数 | 中位数 | 众数 |
七 | 84.1 | _______ | 85 |
八 | 86.3 | 87 | ______ |
得出结论:
(1)根据上述数据,将表格补充完整;
(2)估计该校七、八两个年级学生在本次测试成绩中可以取得优秀的人数![]() 共有多少人?
共有多少人?
(3)你认为哪个年级知识掌握的总体水平较好,说明理由.