题目内容
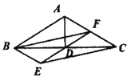
【题目】如图,![]() 中,
中,![]() ,
,![]() 是
是![]() 的角平分线,点
的角平分线,点![]() 为
为![]() 的中点,连接
的中点,连接![]() 并延长到点
并延长到点![]() ,使
,使![]() ,连接
,连接![]() ,
,![]() 和
和![]() .
.
(1)求证:![]() ;
;
(2)判断并证明四边形![]() 的形状;
的形状;
(3)为![]() 添加一个条件______,则四边形
添加一个条件______,则四边形![]() 是矩形(填空即可,不必说明理由).
是矩形(填空即可,不必说明理由).
【答案】(1)见解析;(2)四边形![]() 为平行四边形,证明见解析;(3)
为平行四边形,证明见解析;(3)![]() (答案不唯一).
(答案不唯一).
【解析】
(1)根据等腰三角形的性质得BD=CD,由对顶角相等得∠BDE=∠CDF,结合已知FD=ED可证出△BDE≌△CDF,即可得BE=FC;
(2)由BD=CD,FD=ED,根据平行四边形的判定定理即可得出四边形![]() 为平行四边形;
为平行四边形;
(3)利用对角线相等且互相平分的四边形是矩形的判断方法即可.
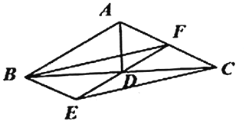
(1)证明:∵![]() ,
,![]() 是
是![]() 的角平分线,
的角平分线,
∴![]() .
.
又∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)四边形![]() 为平行四边形,
为平行四边形,
证明:∵![]() ,
,![]() ,
,
∴四边形![]() 为平行四边形;
为平行四边形;
(3)![]() (答案不唯一)
(答案不唯一)
证明:∵BD=CD,点![]() 为
为![]() 的中点,
的中点,
∴DF=![]() AB,
AB,
∵DF=DE,BD=CD=![]() BC
BC
∴DF=DE=BD=CD,即BC=EF,
∴四边形![]() 为平行四边形.
为平行四边形.
故答案为:(1)见解析;(2)四边形![]() 为平行四边形,证明见解析;(3)
为平行四边形,证明见解析;(3)![]() (答案不唯一).
(答案不唯一).

练习册系列答案
相关题目
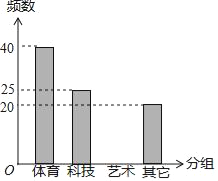
【题目】某学校为调查学生的兴趣爱好,抽查了部分学生,并制作了如下表格与条形统计图:
频数 | 频率 | |
体育 | 40 | 0.4 |
科技 | 25 | a |
艺术 | b | 0.15 |
其它 | 20 | 0.2 |
请根据上图完成下面题目:
(1)总人数为 人,a= ,b= .
(2)请你补全条形统计图.
(3)若全校有600人,请你估算一下全校喜欢艺术类学生的人数有多少?