题目内容
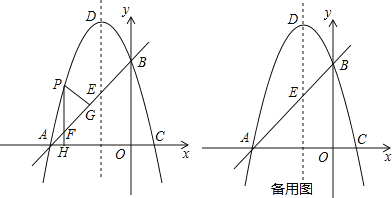
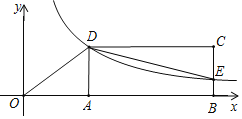
【题目】如图,矩形ABCD的顶点A,B在x轴的正半轴上,反比例函数y=![]() 在第一象限内的图象与直线y=
在第一象限内的图象与直线y=![]() x交于点D,且反比例函数y=
x交于点D,且反比例函数y=![]() 交BC于点E,AD=3.
交BC于点E,AD=3.
(1)求D点的坐标及反比例函数的关系式;
(2)若矩形的面积是24,请写出△CDE的面积(不需要写解答过程).
【答案】(1)D(4,3),y=![]() ,(2)8.
,(2)8.
【解析】
(1)根据AD=3,得到点D的纵坐标为3,代入y=![]() x,解之,求得点D的坐标,再代入y=
x,解之,求得点D的坐标,再代入y=![]() ,得到k的值,即可得到反比例函数的关系式,
,得到k的值,即可得到反比例函数的关系式,
(2)根据“矩形的面积是24”,结合AD=3,求得线段AB,线段CD的长度,得到点B,点C的横坐标,代入反比例函数的解析式,得到点E的坐标,根据“S△CDE=![]() CE×CD”,代入求值即可得到答案.
CE×CD”,代入求值即可得到答案.
解:(1)根据题意得:
点D的纵坐标为3,
把y=3代入y=![]() x得:
x得:
![]() x=3,
x=3,
解得:x=4,
即点D的坐标为:(4,3),
把点D(4,3)代入y=![]() 得:
得:
3=![]() ,
,
解得:k=12,
即反比例函数的关系式为:y=![]() ,
,
(2)设线段AB,线段CD的长度为m,
根据题意得:3m=24,
解得:m=8,
即点B,点C的横坐标为:4+8=12,
把x=12代入y=![]() 得:
得:
y=1,
即点E的坐标为:(3,1),
线段CE的长度为2,
S△CDE=![]() CE×CD
CE×CD
=![]()
=8.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目