题目内容
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴,y轴的正半轴上,且OA=4,OC=3,若抛物线经过O,A两点,且顶点在BC边上,对称轴交AC于点D,动点P在抛物线对称轴上,动点Q在抛物线上.
(1)求抛物线的解析式;
(2)当PO+PC的值最小时,求点P的坐标;
(3)是否存在以A,C,P,Q为顶点的四边形是平行四边形?若存在,请直接写出P,Q的坐标;若不存在,请说明理由.

【答案】(1)y=![]() x2+3x;(2)当PO+PC的值最小时,点P的坐标为(2,
x2+3x;(2)当PO+PC的值最小时,点P的坐标为(2, ![]() );(3)存在,具体见解析.
);(3)存在,具体见解析.
【解析】试题分析:(1)由条件可求得抛物线的顶点坐标及A点坐标,利用待定系数法可求得抛物线解析式;
(2) 连接PA,D与P重合时有最不值,求出点D的坐标即可;
(3)存在,分别以PA,PC、PC,PQ、PA,PQ为一组邻边时,写出坐标即可;
试题解析:
(1)在矩形OABC中,OA=4,OC=3,
∴A(4,0),C(0,3),
∵抛物线经过O、A两点,且顶点在BC边上,
∴抛物线顶点坐标为(2,3),
∴可设抛物线解析式为y=a(x﹣2)2+3,
把A点坐标代入可得0=a(4﹣2)2+3,解得a=![]() ,
,
∴抛物线解析式为y=![]() (x﹣2)2+3,即y=
(x﹣2)2+3,即y=![]() x2+3x;
x2+3x;
(2)连接PA,
∵点P在抛物线对称轴上,∴PA=PO,∴PO+PC= PA+PC.
当点P与点D重合时,PA+PC= AC;
当点P不与点D重合时,PA+PC> AC;
∴当点P与点D重合时,PO+PC的值最小,
设直线AC的解析式为y=kx+b,
根据题意,得![]() 解得
解得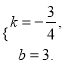
∴直线AC的解析式为![]() ,
,
当x=2时, ![]() ,
,
∴当PO+PC的值最小时,点P的坐标为(2, ![]() );
);
(3)存在.当以PA,PC为一组邻边时,P(2,0),Q(2,3);
当以PC,PQ为一组邻边时,P(2,-6),Q(6,-9);
当以PA,PQ为一组邻边时,P(2,-12),Q(-2,-9).

 轻松暑假总复习系列答案
轻松暑假总复习系列答案