题目内容
【题目】如图,已知点A(-1,0)和点B(1,2),在![]() 轴上确定点P,使得△ABP为直角三角形,则满足这样条件的点P的坐标是____________________.
轴上确定点P,使得△ABP为直角三角形,则满足这样条件的点P的坐标是____________________.
【答案】(1,0)或(3,0)
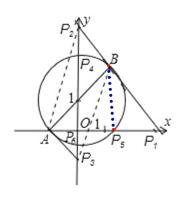
【解析】分析:当∠PBA=90°时,即点P的位置有2个;当∠BPA=90°时,点P的位置有3个;当∠BAP=90°时,在y轴上共有1个交点.
详解:①以A为直角顶点,可过A作直线垂直于AB,此时与y轴交于一点,这一点不合题意,舍去;
②以P为直角顶点,可以AB为直径画圆,与坐标轴共有3个交点,其中P4,P6不合题意舍去,P5点符合要求;
连接BP5,则∠AP5B=90°.
∵点B(1,2),
∴P5(1,0).
③以B为直角顶点,可过B作直线垂直于AB,与坐标轴交于两点,P2不合题意舍去,P1点符合要求;
∵点A(-1,0),点B(1,2),点P5(1,0)
∴AP5=2,BP5=2,
∴AP5=BP5=2,
∴△ABP5是等腰直角三角形,
∴∠AP5B=45°,
∴∠BP1P5=45°,
∴P1P5= BP5=2,
∴OP1=OP5+ P1P5=3,
∴P1 (3,0).
故答案为:(1,0)或(3,0).

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目