��Ŀ����
����Ŀ�����壺���ڸ����Ķ��κ���y=a��x��h��2+k��a��0���������һ�κ���Ϊy=a��x��h��+k�����磺���κ���y=2��x+1��2��3�İ���һ�κ���Ϊy=2��x+1����3����y=2x��1��
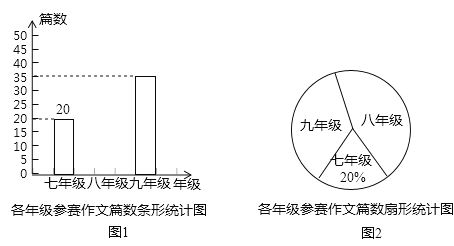
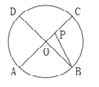
��1����֪���κ���y=��x��1��2��4���������һ�κ����ı���ʽΪ_____��
��2����˵�����κ���y=��x��1��2��4�Ķ����������һ�κ�����ͼ���ϣ�
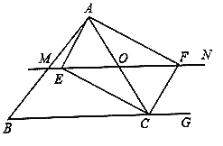
��3����ͼ�����κ���y=m��x��1��2��4m��m��0���İ���һ�κ�����ͼ����x�ᡢy��ֱ��ڵ�B��A����������ͼ��Ľ���ĺ�����ֱ�Ϊ1��2���ڡ�AOB�ڲ��Ķ��κ���y=m��x��1��2��4m��ͼ������һ����P������P��x���ƽ�����������һ�κ�����ͼ���ڵ�Q�����P�ĺ�����Ϊn��ֱ��д���߶�PQ�ij�Ϊ![]() ʱn��ֵ��
ʱn��ֵ��

���𰸡�y=x��5
����������������1�����ݶ��壬ֱ�ӱ��εõ�����һ�κ����Ľ���ʽ��
��2��������㣬���������������ʽ������⣻
��3����������õ�������������ʽ������P������꣬�����ʾ�������꣬Ȼ��ͨ��PQ��x���ƽ�й�ϵ�����Q������꣬��PQ�ij��з�����⼴��.
��⣺��1���߶��κ���y=��x��1��2��4��
�������һ�κ����ı���ʽΪy=��x��1����4=x��5��
�ʴ�Ϊy=x��5��
��2���߶��κ���y=��x��1��2��4��
�ඥ������Ϊ��1����4����
�߶��κ���y=��x��1��2��4��
�������һ�κ����ı���ʽΪy=x��5��
�൱x=1ʱ��y=1��5=��4��
�ࣨ1����4����ֱ��y=x��5�ϣ�
�������κ���y=��x��1��2��4�Ķ����������һ�κ�����ͼ���ϣ�
��3���߶��κ���y=m��x��1��2��4m��
�������һ�κ���Ϊy=m��x��1����4m=mx��5m��
��P��ĺ�����Ϊn����n��2����
��P��������Ϊm��n��1��2��4m��
����P��n��m��n��1��2��4m����
��PQ��x�ᣬ
��Q����n��1��2+1��m��n��1��2��4m����
��PQ=��n��1��2+1��n��
���߶�PQ�ij�Ϊ![]() ��
��
�ࣨn��1��2+1��n=![]() ��
��
��n=![]() ��
��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��Ϊ�˹᳹��ʵ��ί���������������ƶ������ijУ���ƶ���һϵ�а��A��B��ƶ����ļƻ����־�����ij������152�����絽A��B������ֳ�����ô�С������15������ǡ����һ���������������磬��֪�����ִ�С�������ػ������ֱ�Ϊ12��/����8��/����������A��B������˷������
���� | Ŀ�ĵ� | |
A�壨Ԫ/���� | B�壨Ԫ/���� | |
����� | ||
800 | 900 | |
���� | 400 | 600 |
��1������15�����д�С��������������
��2���ְ�������10������ǰ��A�壬�������ǰ��B�壬��ǰ��A��Ĵ����Ϊx����ǰ��A��B�����ܷ���ΪyԪ�������y��x�ĺ�������ʽ��
��3���ڣ�2���������£�������A������粻����100�䣬����д��ʹ�ܷ������ٵĻ������䷽������������ٷ��ã�