МвДҝДЪИЭ
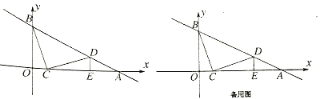
ЎҫМвДҝЎҝИзНј,ФЪЖҪГжЦұҪЗЧшұкПөЦР,ЦұПЯ y=kx+bУлx ЦбЎўy ЦбПаҪ»ёЙA(6Ј¬0)Ј¬B(0Ј¬3)БҪөгЈ¬¶ҜөгCФЪПЯ¶ОOAЙП,Ҫ«ПЯ¶ОCB ИЖЧЕөгCЛіКұХлРэЧӘ90ЎгөГөҪCD,ҙЛКұөгDЗЎәГВдФЪЦұПЯABЙП,№эөгD ЧчDEЎНx ЦбУЪөгE
(1)ЗуЦұПЯy=kx+b өДұнҙпКҪј°өгD өДЧшұкЈ»
(2)ИфөгPФЪy ЦбЙП,өгQФЪЦұПЯABЙП,КЗ·сҙжФЪТФCЎўDЎўPЎўQ ОӘ¶ҘөгөДЛДұЯРОКЗЖҪРРЛДұЯРОЈҝИфҙжФЪ,ЦұҪУРҙіцЛщУРВъЧгМхјюөДQ өгЧшұкЈ¬ИфІ»ҙжФЪ,ЗлЛөГчАнУЙ.
Ўҫҙр°ёЎҝЈЁ1Ј©DЈЁ4Ј¬1Ј©;ЈЁ2Ј©QөДЧшұкОӘ![]()
![]() »т
»т![]()
ЎҫҪвОцЎҝ
ЈЁ1Ј©УГҙэ¶ЁПөКэ·ЁПИЗуіцЦұПЯҪвОцКҪЈ¬УЙРэЧӘҪЗОӘ90ЎгЈ¬ҝЙЦӨөГЎПBCO=ЎПCDEЈ¬ҙУ¶шөГөҪЎчBOCЎХЎчCEDЈ¬ЛщТФOC=DEЈ¬BO=CE=3Ј¬ЙиOC=DE=m, ФтөгDЈЁm+3Ј¬mЈ©Ј¬ҙъИлҪвОцКҪЗуіцm,Ҫш¶шөГөҪөгDөДЧшұк.ЈЁ2Ј©·ЦИэЦЦЗйҝц»ӯіцНјРОЈ¬ҪбәПЖҪРРЛДұЯРОөДРФЦКЗуіцөгөДЧшұкјҙҝЙ.
ҪвЈә
ЈЁ1Ј©Ҫ«AЈЁ6Ј¬0Ј©ЎўBЈЁ0Ј¬3Ј©ҙъИлЦұПЯy=kx+bөГЈ¬
![]()
Ўа
![]() Ј¬
Ј¬
ЎЯЎПBOC=ЎПBCD=ЎПCED=90ЎгЈ¬
ЎаЎПOCB+ЎПDCE=90ЎгЈ¬ЎПDCE+ЎПCDE=90ЎгЈ¬
ЎаЎПBCO=ЎПCDEЈ¬
ЎЯBC=CDЈ¬
ЎаЎчBOCЎХЎчCEDЈ¬
ЎаOC=DEЈ¬BO=CE=3Ј¬
ЙиOC=DE=m,
ЎаDЈЁm+3Ј¬mЈ©
°СDЈЁm+3Ј¬mЈ©ҙъИл![]() өГЈ¬
өГЈ¬
![]() Ј¬
Ј¬
Ўаm=1 Ј¬
ЎаDЈЁ4Ј¬1Ј©Ј¬
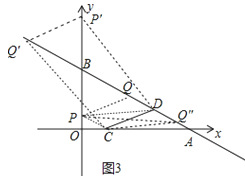
ЈЁ2Ј©ИзНјЈ¬ўЩЧчCPЎОABҪ»yЦбУЪP,ЧчPQЎОCDҪ»ABУЪQ,ФтЛДұЯРОPCDQКЗЖҪРРЛДұЯРОЈ¬Йи![]() ,Ҫ«CЈЁ1Ј¬0Ј©ҙъИлөГЈ¬b=
,Ҫ«CЈЁ1Ј¬0Ј©ҙъИлөГЈ¬b=![]() ,
,
Ўа![]() Ј¬
Ј¬
ЎаPЈЁ0Ј¬![]() Ј©Ј¬
Ј©Ј¬
ЎЯөгCПтУТЖҪТЖ3ёцөҘО»Ј¬ФЩПтЙПЖҪТЖ1ёцөҘО»өГөҪD,
ЎаөгPПтУТЖҪТЖ3ёцөҘО»Ј¬ФЩПтЙПЖҪТЖ1ёцөҘО»өГөҪQ,
ЎаQ![]()
ўЪ ЧчPЎдQЎдЎОCDҪ»yЦбУЪPЎд,Ҫ»ABУЪQЎд,ФтЛДұЯРОQЎдCDPЎдКЗЖҪРРЛДұЯРОЈ¬
ЎЯPQ![]() CDЈ¬PЎдQЎд
CDЈ¬PЎдQЎд![]() CDЈ¬
CDЈ¬
ЎаPQ![]() PЎдQЎдЈ¬
PЎдQЎдЈ¬
ЎаPЎдQЎдPQКЗЖҪРРЛДұЯРОЈ¬
ЎаQЎд,Q№ШУЪөгB¶ФіЖЈ¬
ЎаQЎд![]() Ј¬
Ј¬
ўЫ өұCDОӘ¶ФҪЗПЯКұЈ¬ЛДұЯРОDPCQЎдЎдОӘЖҪРРЛДұЯРОЈ¬
Н¬ўЩЈ¬УЙЖҪТЖҝЙөГQЎдЎд![]() Ј¬
Ј¬
ЎаQөДЧшұкОӘ![]()
![]() »т
»т![]()

 ФД¶БҝміөПөБРҙр°ё
ФД¶БҝміөПөБРҙр°ё