题目内容
【题目】如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接DE,DG.
(1)请判断四边形EBGD的形状,并说明理由;
(2)若∠ABC=60°,∠C=45°,DE=![]() ,求BC的长.
,求BC的长.
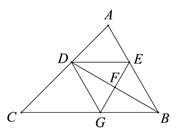
【答案】(1)四边形EBGD为菱形(2)3+3![]()
【解析】试题分析:(1)先证明四边形BEDG为平行四边形,再根据一组邻边相等的平行四边形得出四边形EBGD为菱形.
(2)作EM⊥BC于M,先求得BM和CM的值,再根据BC=BM+CM即可.
试题解析:
(1)四边形EBGD为菱形;
理由:∵EG垂直平分BD,
∴EB=ED,GB=GD,
∴∠EBD=∠EDB,
∵∠EBD=∠DBC,
∴∠EDF=∠GBF,
∴DE∥BG,同理BE∥DG,
∴四边形BEDG为平行四边形,
又∵DE=BE,
∴四边形EBGD为菱形;
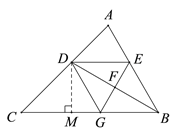
(2)如答图,过D作DM⊥BC于M,由(1)知,∠DGC=∠ABC=60°,∠DBM=![]() ∠ABC=30°,DE=DG=
∠ABC=30°,DE=DG=![]() ,
,
∴在Rt△DMG中,得DM=3,在Rt△DMB中,得BM=![]() ,
,
又∵∠C=45°,
∴CM=DM=3,
∴BC=3+![]() .
.

【题目】为了贯彻落实市委政府提出的“精准扶贫”精神,某校特制定了一系列帮扶A、B两贫困村的计划,现决定从某地运送152箱鱼苗到A、B两村养殖,若用大小货车共15辆,则恰好能一次性运完这批鱼苗,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其运往A、B两村的运费如表:
车型 | 目的地 | |
A村(元/辆) | B村(元/辆) | |
大货车 | ||
800 | 900 | |
小货车 | 400 | 600 |
(1)求这15辆车中大小货车各多少辆?
(2)现安排其中10辆货车前往A村,其余货车前往B村,设前往A村的大货车为x辆,前往A、B两村总费用为y元,试求出y与x的函数解析式.
(3)在(2)的条件下,若运往A村的鱼苗不少于100箱,请你写出使总费用最少的货车调配方案,并求出最少费用.
【题目】王大伯承包了25亩土地,今年春季改种茄子和西红柿两种大棚蔬菜,其中种茄子每亩可获利2400元,种西红柿每亩可获利2600元,王大伯一共获纯利多少元.
(1)若设种茄子x亩,用含有x的式子填下表:
亩数 | 每亩可获利 | 总获利 | |
茄子 | |||
西红柿 |
(2)王大伯种两种蔬菜一共获纯利多少元.(用含x的代数式表示)



