题目内容
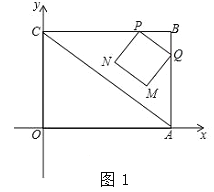
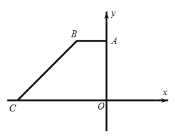
【题目】正方形ABCD和正方形CEFG如图1所示,其中B、C、E在一条直线上,O是AF的中点,连接OD、OG
(1)探究OD与OG的位置关系![]() 的值;(写出结论不用证明)
的值;(写出结论不用证明)
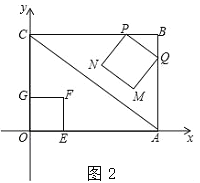
(2)如图2所示,将正方形ABCD和正方形CEFG改为菱形ABCD和菱形CEFG,且∠ABC=∠DCE=120°,探究OD与OG的位置关系,及![]() 的比值;
的比值;
(3)拓展探索:把图1中的正方形CEFG绕C顺时针旋转小于90°的角后,其他条件均不变,问第1问中的两个结论是否发生变化?(写出结论不用证明)

【答案】(1)OD⊥OG. ![]() =1;(2)OD⊥OG,
=1;(2)OD⊥OG, ![]() ,理由见解析;(3)第(1)问中的两个结论没有发生变化.
,理由见解析;(3)第(1)问中的两个结论没有发生变化.
【解析】试题分析:
(1)延长GO交AD于点H,由已知条件易证△AHO≌△FGO,从而可得GO=HO,GF=AH=GC,结合AD=CD可得DH=DG,结合∠GDH=90°即可得到OD⊥OG,OD=OG,从而可得![]() ;
;
(2)延长GO交AD于H,同(1)易证△AHO≌△FGO,从而同理可得OD⊥OG,由已知条件可证得∠ODG=60°,则∠DGO=30°,结合∠DOG=90°,即可得到tan∠DGO=![]() ;
;
(3)第(1)问中的两个结论没有发生变化,如图3,过点F作FH∥AD交DO的延长线于点H,延长DC交FH于点M,连接GH,DG,这样由已知易证△ADO≌△FHO,从而可得FH=AD=CD,DO=HO;再由∠GCE=∠CMN=∠E=∠EFG=90°,可得∠DCG+∠MCN=∠MCN+∠CNM=∠FNE+∠NEF=∠NEF+∠GFH=90°,结合∠CNM=∠FNE可得∠DCG=∠CNM=∠GFH即可证得△DCG≌△HFG,进一步即可证得△DGH是等腰直角三角形,即可由此得到DO=GO,且DO⊥GO,从而说明(1)中结论仍然成立了.
试题解析:
(1)OD⊥OG, ![]() =1,理由如下:
=1,理由如下:
如图1,延长GO交AD于点H,由已知可得OA=OF,AD∥GF,
∴∠OAH=∠OFG,∠AHO=∠FGO,
∴△AHO≌△FGO,
∴OH=OG,AH=GF=GC,
又∵AD=CD,
∴DH=DG,
∴DO⊥OG,
∵∠ADC=90°,∴DO=OG,
∴![]() ;
;

(2)OD⊥OG , ![]() ,理由如下:
,理由如下:
如图2所示,延长GO交AD于H.

∵菱形ABCD和菱形CEFG,且B、C、E在一条直线上,
∴AD∥GF,
∵O是AF的中点,
∴△AOH≌△FOG,
∴AH=CF,HO=OG,
∵CF=CG,AD=CD,
∴DH=DG,
∴DO⊥HG且∠ODG=60°,
∴![]() ;
;
(3)第(1)问中的两个结论没有发生变化,理由如下:
如图3,过点F作FH∥AD交DO的延长线于点H,延长DC交FH于点M,连接GH,DG,
∴∠ADO=∠FHO,∠DAO=∠HFO,
又∵AO=FO,
∴△ADO≌△FHO,
∴FH=AD=CD,DO=HO,
∵∠GCE=∠CMN=∠E=∠EFG=90°,
∴∠DCG+∠MCN=∠MCN+∠CNM=∠FNE+∠NEF=∠NEF+∠GFH=90°,
又∵∠CNM=∠FNE,
∴∠DCG=∠CNM=∠GFH,
又∵DC=FH,CG=FG,
∴△DCG≌△HFG,
∴DG=HG/span>,∠DGC=∠HGF,
∵∠CGH+∠HFG=∠CGF=90°,
∴∠CGH+∠DGC=∠=90°,
∴△DGH是等腰直角三角形,
又∵DO=HO,
∴DO=GO,且DO⊥GO,
∴![]() ,
,
∴(1)中结论仍然成立.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案