题目内容
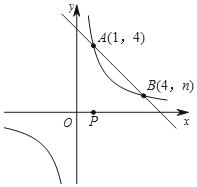
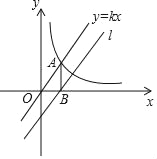
【题目】如图，正比例函数y＝kx与反比例函数y＝
（x＞0）的图象有个交点A，AB⊥x轴于点B．平移正比例函数y＝kx的图象，使其经过点B（2，0），得到直线l，直线l与y轴交于点C（0，﹣3）
（1）求k和m的值；
（2）点M是直线OA上一点过点M作MN∥AB，交反比例函数y＝（x＞0）的图象于点N，若线段MN＝3，求点M的坐标．
【答案】（1）
，m=6 （2）（
，
）或（
， 
）
【解析】
（1）利用待定系数法即可解决问题；(2)设点M（x，
x）,N(x，
)，利用MN//AB， MN=3，列方程求解即可.
（1）∵直线l与y轴交于点(0，-3)，且过点 B(2，0)，
设直线l的解析式为y=ax-3，代入点B(2，0)，解得a=，
∵直线l与正比例函数y=kx平行，∴k=a=，
∵y=x过点 A，AB⊥x轴于点B，∴A(2，3)
∵y=
过点A，∴m=6；
（2）设点M（x，x）,N(x，)，
∵MN//AB， MN=3， ∴ x-=3，或x-=-3，
解得：
，或
(舍去负值)，
∴点M的坐标为（，）或（， 
）
孟建平小学滚动测试系列答案
【题目】某班“数学兴趣小组”对函数y＝
+x的图象与性质进行了探究，探究过程如下，请补充完整．
(1)函数y＝+x的自变量x的取值范围是 ；
(2)下表是y与x的几组对应值．
x | … | ﹣3 | ﹣2 | ﹣1 | 0 |
|
|
|
| 2 | 3 | 4 | 5 | … |
y | … | ﹣ | ﹣ | ﹣ | ﹣1 | ﹣ | ﹣ |
|
| 3 |
| m |
| … |
求m的值；
(3)如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点，根据描出的点，画出该函数的图象；
(4)进一步探究发现，该函数图象在第一象限内的最低点的坐标是(2，3)，结合函数的图象，写出该函数的其它性质(一条即可)： ．
(5)小明发现，①该函数的图象关于点( ， )成中心对称；
②该函数的图象与一条垂直于x轴的直线无交点，则这条直线为 ；
③直线y＝m与该函数的图象无交点，则m的取值范围为 ．
