��Ŀ����
����Ŀ�����壺��ͼ�٣�������y��ax2��bx��c(a��0)��x�ύ��A��B���㣬��P�ڸ���������(P����A��B���㲻�غ�)�������ABP����������AP2��BP2��AB2����Ƶ�PΪ������y��ax2��bx��c(a��0)�Ĺ��ɵ㣮
(1)ֱ��д��������y����x2��1�Ĺ��ɵ�����꣮
(2)��ͼ�ڣ���֪������y��ax2��bx(a��0)��x�ύ��A��B���㣬��P(1�� ![]() )�������ߵĹ��ɵ㣬�������ߵĺ�������ʽ��
)�������ߵĹ��ɵ㣬�������ߵĺ�������ʽ��
(3)��(2)�������£���Q���������ϣ�����������S��ABQ��S��ABP��Q��(���ڵ�P)�����꣮

���𰸡�(1)(0��1)(2) y��-![]() x(x-4)��-
x(x-4)��-![]() x2��
x2��![]() x(3)���������ĵ�Q��3�����ֱ�Ϊ(3��
x(3)���������ĵ�Q��3�����ֱ�Ϊ(3�� ![]() )��(2��
)��(2��![]() ����
���� ![]() )��(2��
)��(2��![]() ����
���� ![]() )��
)��
���������������:(1)���������߹��ɵ�Ķ���������,(2)��PG��x��,�ɵ�P���������:AG=1,PG=![]() ,�����Ǻ����ɵ�:
,�����Ǻ����ɵ�: ![]() ,��֪��PAG=60���Ӷ����AB=4,��B(4,0),����ϵ����������,(3)��
,��֪��PAG=60���Ӷ����AB=4,��B(4,0),����ϵ����������,(3)��![]() ������������ͬ��,��֪��Q��x��ľ���Ϊ
������������ͬ��,��֪��Q��x��ľ���Ϊ![]() ,�������.
,�������.
(1)������y����x2��1�Ĺ��ɵ������Ϊ(0��1)��
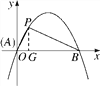
(2)��ͼ����PG��x���ڵ�G.�ߵ�P������Ϊ(1��![]() )����AG��1��PG��
)����AG��1��PG��![]() ����PA��
����PA��![]() ��
��![]() ��2.��tan��PAB��
��2.��tan��PAB��![]() ��
��![]() �����PAG��60��.��Rt��PAB��AB��
�����PAG��60��.��Rt��PAB��AB��![]() ��
��![]() ��4�����B������Ϊ(4��0)��
��4�����B������Ϊ(4��0)��
��y��ax(x��4)������P(1��![]() )�����a����
)�����a����![]() ����y����
����y����![]() x(x��4)����
x(x��4)����![]() x2��
x2��![]() x.
x.
(3)�ٵ���Q��x���Ϸ�ʱ����S��ABQ��S��ABP֪��Q��������Ϊ![]() �����У�
������![]() x2��
x2��![]() x��
x��![]() �����x1��3��x2��1(���������⣬��ȥ)�����Q������Ϊ(3��
�����x1��3��x2��1(���������⣬��ȥ)�����Q������Ϊ(3��![]() )��
)��
�ڵ���Q��x���·�ʱ����S��ABQ��S��ABP֪��Q��������Ϊ��![]() �����У�
������![]() x2��
x2��![]() x����
x����![]() �����x1��2��
�����x1��2��![]() ��x2��2��
��x2��2��![]() �����Q������Ϊ(2��
�����Q������Ϊ(2��![]() ����
����![]() )��(2��
)��(2��![]() ����
����![]() )��
)��
�������������������ĵ�Q��3�����ֱ�Ϊ(3��![]() )��(2��
)��(2��![]() ����
����![]() )��(2��
)��(2��![]() ����
����![]() )��
)��

