题目内容
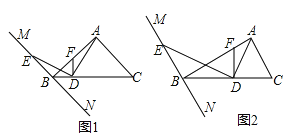
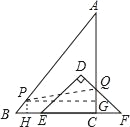
【题目】已知,把Rt△ABC和Rt△DEF按图1摆放,(点C与E点重合),点B、C、E、F始终在同一条直线上,∠ACB=∠EDF=90°,∠DEF=45°,AC=8,BC=6,EF=10,如图2,△DEF从图1出发,以每秒1个单位的速度沿CB向△ABC匀速运动,同时,点P从A出发,沿AB以每秒1个单位向点B匀速移动,AC与△DEF的直角边相交于Q,当P到达终点B时,△DEF同时停止运动,连接PQ,设移动的时间为t(s).解答下列问题:
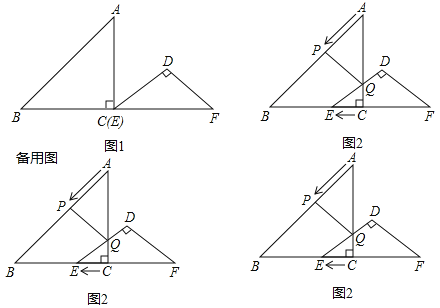
(1)△DEF在平移的过程中,当点D在Rt△ABC的边AC上时,求t的值;
(2)在移动过程中,是否存在△APQ为等腰三角形?若存在,求出t的值;若不存在,说明理由.
(3)在移动过程中,当0<t≤5时,连接PE,是否存在△PQE为直角三角形?若存在,求出t的值;若不存在,说明理由.
【答案】(1)t=5;(2)见解析;(3)见解析.
【解析】
(1)根据等腰三角形性质求出即可;(2)①AP=AQ,求出即可;②AP=PQ,作PH⊥AC于H,根据相似得出比例式,即可求出答案;③AQ=PQ,作PH⊥AC于H,根据相似得出比例式,④当5≤t≤10时,AQ=PQ,作PH⊥BC,PG⊥AC,利用相似与勾股定理,即可求出答案;(3)分为三种情况,①∠PQE=90°,②∠PEQ=90°,③∠EPQ=90°,根据勾股定理得出方程,求出方程的解,看是否满足小于10即可.
(1)当D在AC上时,
∵DE=DF,
∴EC=CF=![]() EF=5,
EF=5,
∴t=5.
(2)存在.
∵AP=t,∠EDF=90°,∠DEF=45°,
∴∠CQE=45°=∠DEF,
∴CQ=CE=t,
AQ=8﹣t,
当0≤t<5时,
①AP=AQ,
t=8﹣t,
∴t=4;
②AP=PQ,
作PH⊥AC于H,
AH=HQ=![]() AQ=4﹣
AQ=4﹣![]() t,
t,
∵PH∥BC,
∴△APH∽△ABC,
∴![]() ,
,
∴![]() ,
,
∴t=![]() ;
;
③AQ=PQ,
作QI⊥AB于I,
AI=PI=![]() AP=
AP=![]() t(等腰三角形的性质三线合一),
t(等腰三角形的性质三线合一),
∵∠AIQ=∠ACB=90°,∠A=∠A,
∴△AIQ∽△ACB,
∴![]() ,
,
∴![]() ,
,
∴t=![]() ,
,
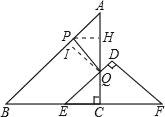
④当5≤t≤10时,AQ=PQ,作PH⊥BC,PG⊥AC,连接PQ,
同理可求出:
FC=QC=10﹣t,BP=10﹣t,
PH=![]() (10﹣t)=8﹣
(10﹣t)=8﹣![]() t,
t,
BH=![]() (10﹣t)=6﹣
(10﹣t)=6﹣![]() t,
t,
QG=QC﹣GC=QC﹣PH=10﹣t﹣(8﹣![]() t)=2﹣
t)=2﹣![]() ,
,
PG=HC=6﹣(6﹣![]() t)=
t)=![]() t,
t,
PQ=AQ=8﹣(10﹣t)=t﹣2,
∴PQ 2=PG 2+QG 2,
(t﹣2)2=(![]() t) 2+(2﹣
t) 2+(2﹣![]() ) 2,
) 2,
解得:t=![]() 秒,
秒,
其它情况不符合要求,
综合上述:当t等于4秒、![]() 秒、
秒、![]() 秒、
秒、![]() 秒时△APQ是等腰三角形.
秒时△APQ是等腰三角形.
(3)作PW⊥AC于W,PH⊥BC于H,
由勾股定理:CE=CQ=t,
∵sinA=![]() =
=![]() =
=![]() ,cosA=
,cosA=![]() =
=![]() =
=![]() ,
,
∴PW=![]() t,AW=
t,AW=![]() t,
t,
∴QW=8﹣![]() t﹣t=8﹣
t﹣t=8﹣![]() t,
t,
∴PQ2=PM2+QW2=(![]() t)2+(8﹣
t)2+(8﹣![]() t)2=
t)2=![]() t2﹣
t2﹣![]() t+64,
t+64,
PE2=PH2+EH2=(t+8﹣![]() t)2+(t﹣
t)2+(t﹣![]() t)2=
t)2=![]() t2﹣
t2﹣![]() t+64,
t+64,
QE2=2t2
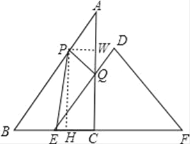
①∠PQE=90°,
在Rt△PEQ中
PQ2+QE2=PE2,
即![]() t2﹣
t2﹣![]() t+64+2t2=
t+64+2t2=![]() t2﹣
t2﹣![]() t+64,
t+64,
解得:t1=0(舍去),t2=![]() ;
;
②∠PEQ=90°,
PE2+EQ2=PQ2
即![]() t2﹣
t2﹣![]() t+64+2t2=
t+64+2t2=![]() t2﹣
t2﹣![]() t+64,
t+64,
解得:t1=0(舍去),t2=20(舍去)
∴此时不存在;
③当∠EPQ=90°时
PQ2+PE2=EQ2,
即![]() t2﹣
t2﹣![]() t+64+
t+64+![]() t2﹣
t2﹣![]() t+64=2t2,
t+64=2t2,
t1=![]() (舍去),t2=4,
(舍去),t2=4,
综合上述:当t=![]() 或t=4时,△PQE是直角三角形.
或t=4时,△PQE是直角三角形.