题目内容
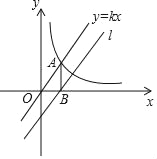
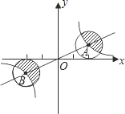
【题目】如图,正比例函数与反比例函数的图象相交于AB、两点,分别以AB、两点为圆心,画与x轴相切的两个圆,若点A的坐标为(2,1),则图中两个阴影部分面积的和是( )
A. ![]() B.
B. ![]() C. π D. 4π
C. π D. 4π
【答案】C
【解析】
先利用切线的性质得到⊙A的半径为1,再根据反比例函数图象的对称性得到点B的坐标为(-2,-1),同理得到⊙B的半径为1,则可判断⊙A与⊙B关于原点中心对称,⊙A的阴影部分与⊙B空白的部分的面积相等,所以图中两个阴影部分面积的和等于⊙A的面积,然后根据圆的面积公式计算.
解:∵点A的坐标为(2,1),且⊙A与x轴相切,
∴⊙A的半径为1,
∵点A和点B是正比例函数与反比例函数的图象的交点,
∴点B的坐标为(-2,-1),
同理得到⊙B的半径为1,
∴⊙A与⊙B关于原点中心对称,
∴⊙A的阴影部分与⊙B空白的部分完全重合,
∴⊙A的阴影部分与⊙B空白的部分的面积相等,
∴图中两个阴影部分面积的和=π12=π.
故选:C.

练习册系列答案
相关题目