题目内容
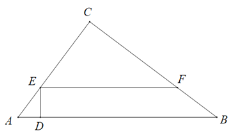
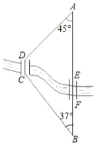
【题目】如图,A,B两地之间有条河,原来从A地到B地需要经过桥DC,沿折线A→D→C→B到达,现在新建了桥EF,可直接沿直线AB从A地到达B地.已知BC=11km,∠A=45°,∠B=37°,桥DC和AB平行,桥DC与桥EF的长相等.
(1)求点D到直线AB的距离;
(2)现在从A地到B地可比原来少走多少路程?
(结果保留小数点后一位.参考数据:![]() ≈1.41,sin37°≈0.60,cos37°≈0.80).
≈1.41,sin37°≈0.60,cos37°≈0.80).
【答案】(1)6.60;(2)4.9
【解析】
(1)过点D作DH⊥AB于H,DG∥CB交AB于G,根据平行四边形的判定得出DCBG为平行四边形,在Rt△DGH中,根据DH=DGsin37,即可求出点D到直线AB的距离;
(2)根据(1)先求出GH、AD和AH的长,再根据两条路线路程之差为AD+DG-AG,代值计算即可得出答案.
解:(1)如图,过点D作DH⊥AB于H,DG∥CB交AB于G,
∵DC∥AB,
∴四边形DCBG为平行四边形.
∴DC=GB,GD=BC=11.
在Rt△DGH中,
DH=DGsin37°≈11×0.60=6.60,
∴点D到直线AB的距离是6.60km;
(2)根据(1)得:
GH=DGcos37°≈11×0.80≈8.80,
在Rt△ADH中,
AD=![]() DH≈1.41×6.60≈9.31.
DH≈1.41×6.60≈9.31.
AH=DH≈6.60,
∵两条路线路程之差为AD+DG﹣AG,
∴AD+DG﹣AG=(9.31+11)﹣(6.60+8.80)≈4.9(km).
即现在从A地到B地可比原来少走约4.9km.

练习册系列答案
相关题目