题目内容
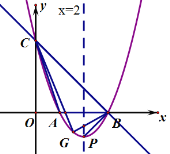
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(![]() ,0)和(m,y),对称轴为直线x=﹣1,下列5个结论:其中正确的结论为_____.(注:只填写正确结论的序号)①abc>0;②a+2b+4c=0;③2a﹣b>0;④3b+2c>0;⑤a﹣b≥m(am﹣b)
,0)和(m,y),对称轴为直线x=﹣1,下列5个结论:其中正确的结论为_____.(注:只填写正确结论的序号)①abc>0;②a+2b+4c=0;③2a﹣b>0;④3b+2c>0;⑤a﹣b≥m(am﹣b)
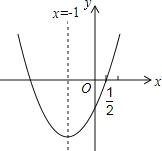
【答案】②④.
【解析】
根据抛物线开口方向得到![]() ,根据抛物线对称轴为直线
,根据抛物线对称轴为直线![]() ,得到
,得到![]() ,则
,则![]() ,根据抛物线与y轴的交点在x轴下方得到
,根据抛物线与y轴的交点在x轴下方得到![]() ,所以
,所以![]() ;由
;由![]() ,
,![]() ,得到
,得到![]() ,即
,即![]() ;由
;由![]() ,
,![]() ,得到
,得到![]() ,即
,即![]() ;由
;由![]() 时,函数值最小,则
时,函数值最小,则![]() ,即
,即![]() .
.
解:∵抛物线开口向上
∴![]()
∵抛物线对称轴为直线![]()
∴![]() ,则
,则![]() ,所以③错误;
,所以③错误;
∴![]()
∵抛物线与![]() 轴的交点在
轴的交点在![]() 轴下方
轴下方
∴![]()
∴![]() ,所以①错误;
,所以①错误;
∵![]() 时,
时,![]()
∴![]() ,即
,即![]() ,所以②正确;
,所以②正确;
∵![]() ,
,![]()
∴![]() ,即
,即![]() ,所以④正确;
,所以④正确;
∵![]() 时,函数值最小
时,函数值最小
∴![]()
∴![]() ,所以⑤错误.
,所以⑤错误.
故答案是:②④

练习册系列答案
相关题目
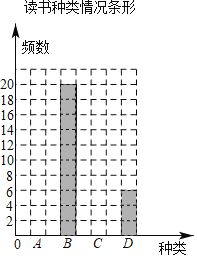
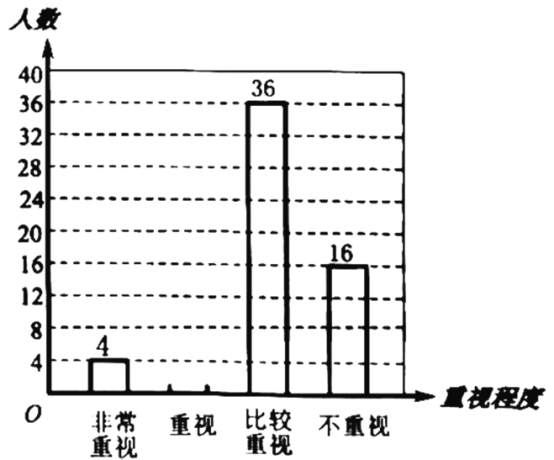
【题目】寒假中,某校七年级开展“阅读经典,读一本好书”的活动.为了解学生阅读情况,从全年级学生中随机抽取了部分学生调查读书种类情况,并进行统计分析,绘制了如下不完整的统计图表:
读书种类情况统计表
种类 | 频数 | 百分比 |
A.科普类 | a | 32% |
B.文学类 | 20 | 40% |
C.艺术类 | 8 | b |
D.其他类 | 6 | 12% |
请根据以上信息,解答下列问题:
(1)填空:a= ,b= ,并补全条形统计图;
(2)若绘制“阅读情况扇形统计图”,则“艺术类”所对应扇形的圆心角度数为 °;
(3)若该校七年级共有800人,请估计全年级在本次活动中读书种类为“艺术类”的学生人数.