题目内容
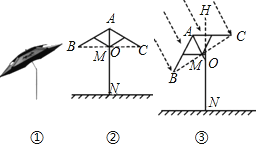
【题目】为了测量大楼顶上(居中)避雷针BC的长度,在地面上点A处测得避雷针底部B和顶部C的仰角分别为55°58′和57°,已知点A与楼底中间部位D的距离约为80米,求避雷针BC的长度.(参考数据:sin55°58′≈0.83,cos55°58′≈0.56,tan55°58′≈1.48,sin57°≈0.84,tan57°≈1.54)
【答案】避雷针BC的长度为4.8米.
【解析】
解直角三角形求出CD,BD,根据BC=CD-BD求解即可.
解:在Rt△ABD中,∵![]() ,
,
∴1.48=![]() ,
,
∵AD=80米,
∴BD=118.4(米),
在Rt△CAD中,∵tan∠CAD=![]() ,
,
∴1.54=![]() ,
,
∴CD=123.2(米),
∴BC=CD-BD=4.8(米)
答:避雷针BC的长度为4.8米.

练习册系列答案
相关题目
【题目】二次函数y=ax2+bx+c(a,b,c是常数,且a≠0)中的x与y的部分对应值如表所示,则下列结论中,正确的个数有( )
x | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
①a<0;②当x<0时,y<3;③当x>1时,y的值随x值的增大而减小;④方程ax2+bx+c=5有两个不相等的实数根.
A.4个B.3个C.2个D.1个