Question

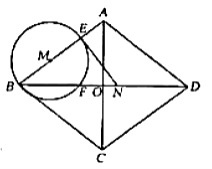
【题目】如图，四边形ABCD的对角线AC、BD交于点O，已知O是AC的中点，AE=CF，DF∥BE．

（1）求证：△BOE≌△DOF；

（2）若OD=OC，则四边形ABCD是什么特殊四边形？请直接给出你的结论，不必证明．

Answer 1

【答案】（1）详见解析；（2）若OD=OC，则四边形ABCD是矩形．

【解析】试题分析：（1）根据平行线的性质证明∠DFO=∠BEO，由O为AC的中点和AE=CF，证明OE=OF，根据ASA即可证得；

（2）根据全等三角形的性质，证明OB=OD，根据对角线互相平分且相等的四边形是矩形即可得证．

（1）证明：∵DF∥BE，

∴∠FDO=∠EBO，∠DFO=∠BEO，

∵O为AC的中点，即OA=OC，AE=CF，

∴OA﹣AE=OC﹣CF，即OE=OF，

在△BOE和△DOF中，

，

∴△BOE≌△DOF（AAS）；

（2）若OD=OC，则四边形ABCD是矩形．

理由是：∵△BOE≌△DOF，

∴OB=OD，

又∵OA=OC，OD=OC，

∴OA=OC= OB=OD，

∴四边形ABCD是矩形．