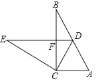
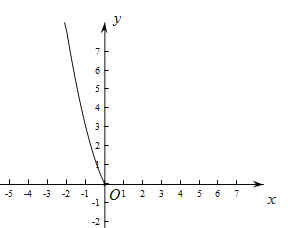题目内容
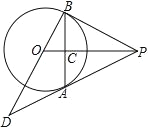
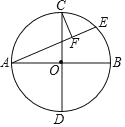
【题目】如图，在⊙O 中，AB、CD是互相垂直的两条直径，点E在
上，CF⊥AE 于点F，若点F四等分弦AE，且AE＝8，则⊙O 的面积为______．
【答案】
π
【解析】
延长CF交AB于点G,连接BE,证明
AFG
COG
推出
，即可求出FG,在RtAFG中，由勾股定理即可得出答案.
延长CF交AB于点G,连接BE,如图
CF⊥AE，
AEB=90 
，且F为四等分弦.
G也为AB的四等分点.即AG= 
AB
设圆的半径为R.
在RtCOG中，由勾股定理，得
CG=
= 
R.
在AFC和COG中，AFC=COG=90，AGF=CGO，
AFG COG
，即GF=
=
=
.
又AF=6， RtAFG中，由勾股定理得，62+（）2=（
）2
解得R2= ，故圆的面积为π.
故答案为：π.
练习册系列答案
阅读快车系列答案
相关题目
【题目】探究函数
的图象与性质.
(1)下表是y与x的几组对应值.
| … |
|
|
|
|
|
|
| … |
| … |
|
|
|
|
|
|
| … |
其中m的值为_______________；
(2)根据上表数据，在如图所示的平面直角坐标系中描点，并已画出了函数图象的一部分，请你画出该图象的另一部分；
(3)结合函数的图象，写出该函数的一条性质：_____________________________；
(4)若关于x的方程
有2个实数根，则t的取值范围是___________________.
