题目内容
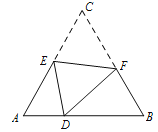
【题目】如图1,在等腰Rt△ABC中,∠C=90°,O是AB的中点,AC=6,∠MON=90°,将∠MON绕点O旋转,OM、ON分别交边AC于点D,交边BC于点E(D、E不与A、B、C重合)
(1)判断△ODE的形状,并说明理由;
(2)在旋转过程中,四边形CDOE的面积是否发生变化?若不改变,直接写出这个值,若改变,请说明理由;
(3)如图2,DE的中点为G,CG的延长线交AB于F,请直接写出四边形CDFE的面积S的取值范围.

【答案】(1)△ODE是等腰直角三角形,理由详见解析;(2)在旋转过程中,四边形CDOE的面积不发生变化,面积为9;(3)0<S≤9.
【解析】
(1)连接OC,根据等腰三角形的性质得到OC⊥AB,OC平分∠ACB,求得∠AOD=∠COE,根据全等三角形的性质即可得到结论;
(2)根据全等三角形的性质得到四边形CDOE的面积=△AOC的面积,根据三角形的面积公式即可得到结论;
(3)当四边形CDFE是正方形时,其面积最大,根据正方形的面积公式即可得到结论.
(1)△ODE是等腰直角三角形,理由如下:
连接OC.在等腰Rt△ABC中,∵O是AB的中点,∴OC⊥AB,OC平分∠ACB,∴∠OCE=45°,OC=OA=OB,∠COA=90°.
∵∠DOE=90°,∴∠AOD=∠COE.在△AOD与△COE中,∵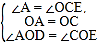 ,∴△AOD≌△COE,(ASA),∴OD=OE,∴△ODE是等腰直角三角形;
,∴△AOD≌△COE,(ASA),∴OD=OE,∴△ODE是等腰直角三角形;
(2)在旋转过程中,四边形CDOE的面积不发生变化.
∵△AOD≌△COE,∴四边形CDOE的面积=△AOC的面积.
∵AC=6,∴AB=6![]() ,∴AO=OC
,∴AO=OC![]() AB=3
AB=3![]() ,∴四边形CDOE的面积=△AOC的面积
,∴四边形CDOE的面积=△AOC的面积![]() 9;
9;
(3)当四边形CDFE是正方形时,其面积最大,四边形CDFE面积的最大值=9,故四边形CDFE的面积S的取值范围为:0<S≤9.

 名校课堂系列答案
名校课堂系列答案