题目内容
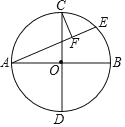
【题目】如图，PA 为⊙O 的切线，A 为切点，过 A 作弦 AB⊥OP，垂足为点 C，延长BO 与 PA 的延长线交于点 D
(1) 求证：PB 为⊙O 的切线
(2) 若 OB＝3，OD＝5，求 PB 的长
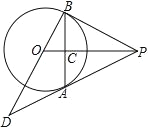
【答案】(1) 见详解；(2) PB=6.
【解析】
(1) 连接OA，根据垂径定理，得到PB=PA，可证明△PAO≌△PBO，因为PA 为⊙O 的切线，所以∠PBO=∠PAO=90°，题目得证；
(2)用勾股定理算出AD，由(1)中△PAO≌△PBO，得到PA=PB，设PB=x，△BDP为直角三角形，利用勾股定理列出等式，求解得出x，即为PB的长.
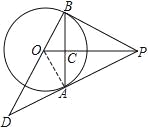
(1)证明：连接OA，
∵PA为⊙O的切线，
∴OA⊥PA
∴∠PAO=90°，
∵OA=OB，OP⊥AB于C，
∴PB=PA，
∴△PAO≌△PBO，
∴∠PBO=∠PAO=90°，
∴PB为⊙O的切线；
(2)在直角三角形OAD中，
，
BD=OB+OD=8，
∵△PAO≌△PBO，
∴PA=PB，
设PB=x，
∵PB 为⊙O 的切线，
∴∠DBP=90°，△BDP为直角三角形，
∴BD+BP=DP2，即8+x=(4+x)，
解得x=6，
∴PB=6.
练习册系列答案
相关题目
