题目内容
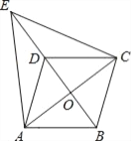
【题目】如图,将一对直角三角形卡片的斜边AC重合摆放,直角顶点B,D在AC的两侧,连接BD,交AC于点O,取AC,BD的中点E,F,连接EF.若AB=12,BC=5,且AD=CD,则EF的长为_____.

【答案】![]() .
.
【解析】
先求出BE的值,作DM⊥AB,DN⊥BC延长线,先证明△ADM≌△CDN(AAS),得出AM=CN,DM=DN,再根据正方形的性质得BM=BN,设AM=CN=x,BM=AB-AM=12-x=BN=5+x,求出x=![]() ,BN=
,BN=![]() ,根据BD为正方形的对角线可得出BD=
,根据BD为正方形的对角线可得出BD=![]()
![]() , BF=
, BF=![]() BD=
BD=![]()
![]() , EF=
, EF=![]() =
=![]()
![]() .
.
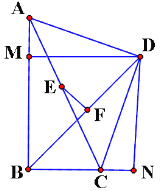
∵∠ABC=∠ADC,
∴A,B,C,D四点共圆,
∴AC为直径,
∵E为AC的中点,
∴E为此圆圆心,
∵F为弦BD中点,
∴EF⊥BD,
连接BE,∴BE=![]() AC=
AC=![]()
![]() =
=![]()
![]() =
=![]() ;
;
作DM⊥AB,DN⊥BC延长线,∠BAD=∠BCN,
在△ADM和△CDN中,
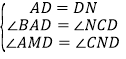 ,
,
∴△ADM≌△CDN(AAS),
∴AM=CN,DM=DN,
∵∠DMB=∠DNC=∠ABC=90°,
∴四边形BNDM为矩形,
又∵DM=DN,
∴矩形BNDM为正方形,
∴BM=BN,
设AM=CN=x,BM=AB-AM=12-x=BN=5+x,
∴12-x=5+x,x=![]() ,BN=
,BN=![]() ,
,
∵BD为正方形BNDM的对角线,
∴BD=![]() BN=
BN=![]()
![]() ,BF=
,BF=![]() BD=
BD=![]()
![]() ,
,
∴EF=![]() =
=![]() =
=![]()
![]() .
.
故答案为![]()
![]() .
.

练习册系列答案
相关题目