题目内容
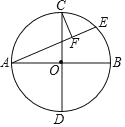
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按逆时针方向旋转n度后,得到△DEC,点D刚好落在AB边上,
(1)求n的值;
(2)若AC=4,求DF的长.
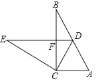
【答案】(1)n=60°;(2)2.
【解析】
(1)由旋转的性质,证明△DAC是等边三角形,即可求得旋转角n的度数;
(2)易得△DFC是含30°角的直角三角形,则可求得DF;
(1)∵将△ABC绕点C按逆时针方向旋转n度后得到△EDC,
∴AC=CD,
∵在Rt△ABC中,∠ACB=90°,∠B=30°,
∴∠A=90°﹣∠B=60°,
∴△DAC是等边三角形,
∴n=∠DCA=60°,
(2)∵∠DCA=60°
∴∠DCB=90°﹣∠DCB=90°﹣60°=30°,
∵AC=4,
∴DC=4,
∵∠FDC=∠B=60°,
∴∠DFC=90°,
∴DF=![]() DC=2,
DC=2,

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目