题目内容
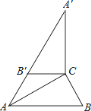
【题目】如图,△ABC 中,∠C=90°,将△ABC 绕点 C 顺时针旋转 90°,得到△DEC(其中点 D、E 分别是 A、B 两点旋转后的对应点).
(1)请画出旋转后的△DEC;
(2)试判断 DE 与 AB 的位置关系,并证明你的结论.
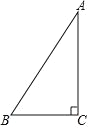
【答案】(1)见解析;(2) DE⊥AB,理由见解析.
【解析】
(1)根据旋转变换得到图形;(2)延长 DE 交 AB 于点 F,证明∠AFE=∠DCE=90°即可.
(1)旋转后的△DEC 如图所示.
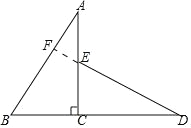
(2)结论:DE⊥AB.
理由:延长 DE 交 AB 于点 F.
由旋转不变性可知:∠A=∠D,∠ACB=∠DCE=90°,
∵∠AEF=∠DEC,
∠∠AFE=∠DCE=90°,
∴DE⊥AB.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目