Question

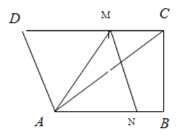
【题目】如图，在直角梯形ABCD中，AB∥DC，∠B=90°，AB=16，BC=12，CD=21．动点M从点C出发，沿射线CD方向以每秒2个单位长的速度运动；动点N从B出发，在线段BA上，以每秒1个单位长的速度向点A运动，点M、N分别从C、B同时出发，当点N运动到点A时，点M随之停止运动．设运动时间为t(秒)．

（1）设△AMN的面积为S，求S与t之间的函数关系式，并确定t的取值范围；

（2）当t为何值时，以A、M、N三点为顶点的三角形是等腰三角形？

Answer 1

【答案】（1）；（2）t=3.5或t=

【解析】

（1）过点M作MH⊥AB，垂足为H，用含的代数式表示的长，再利用三角形面积公式即可得到答案．（2）先用含的代数式分别表示的长，进行分类讨论，利用腰相等建立方程求解．

（1）如图，过点M作MH⊥AB，垂足为H，则四边形BCMH为矩形．

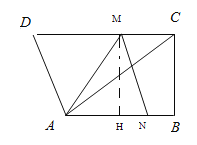
∴MH=BC=12．

∵AN=16-t，

∴；

（2）由（1）可知：BH=CM=2t，BN=t，．

以A、M、N三点为顶点的三角形是等腰三角形，可以分三种情况：

①若MN=AN．因为：

在Rt△MNH中，，所以：MN2=t2+122，

由MN2=AN2得t2+122=（16-t）2，

解得t=．

②若AM=AN．

在Rt△MNH中，AM2=（16-2t）2+122．

由AM2=AN2得：，

即3t2-32t+144=0．

由于△=，

∴3t2-32t+144=0无解，

∴．

③若MA=MN．

由MA2=MN2，得t2+122=（16-2t）2+122

整理，得3t2-64t+256=0．

解得，t2=16（舍去）

综合上面的讨论可知：当t=秒或t=秒时，以A、M、N三点为顶点的三角形是等腰三角形．