题目内容
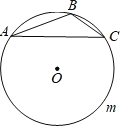
【题目】如图,△ABC中,∠ABC=120°,AC=2,⊙O是△ABC的外接圆,D是![]() 上任意一点(不包括点A、C),顺次连接四边形ABCD四边中点得到四边形EFGH,则四边形EFGH的周长的最大值为____________.
上任意一点(不包括点A、C),顺次连接四边形ABCD四边中点得到四边形EFGH,则四边形EFGH的周长的最大值为____________.
【答案】![]() .
.
【解析】
根据圆内接四边形的性质得到∠D=60°,连接OA,OC,过O作OM⊥AC于M,解直角三角形求出OA的值,如图2,四边形EFGH是边形ABCD的中点四边形,根据三角形的中位线的性质得到EF=HG=![]() AC,EH=FG=
AC,EH=FG=![]() BD,于是得到结论.
BD,于是得到结论.
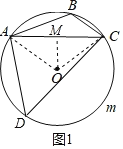
如图1.
∵四边形ABCD 是圆内接四边形,∠ABC=120°,∴∠D=60°,
连接OA,OC,∴∠AOC=120°,
过O作OM⊥AC于M,
∴∠AOM![]() AOC=60°,AM
AOC=60°,AM![]() AC=1,
AC=1,
∴OA![]() ,
,
∴BD![]() .
.
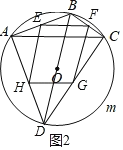
如图2,四边形EFGH是边形ABCD的中点四边形,
∴EF=HG![]() AC,EH=FG
AC,EH=FG![]() BD,
BD,
∴当BD最大时,四边形EFGH的周长的值最大,
∴当BD为⊙O的直径时,四边形EFGH的周长的值最大,
∴四边形EFGH的周长的最大值=EF+HG+HE+GF=AC+BD=2![]() .
.
故答案为:2![]() .
.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案【题目】一粒木质中国象棋子“兵”,它的正面雕刻一个“兵”字,它的反面是平的![]() 将它从一定高度下掷,落地反弹后可能是“兵”字面朝上,也可能是“兵”字面朝下
将它从一定高度下掷,落地反弹后可能是“兵”字面朝上,也可能是“兵”字面朝下![]() 由于棋子的两面不均匀,为了估计“兵”字面朝上的概率,某实验小组做了棋子下掷实验,实验数据如下表:
由于棋子的两面不均匀,为了估计“兵”字面朝上的概率,某实验小组做了棋子下掷实验,实验数据如下表:
实验次数n | 20 | 60 | 100 | 120 | 140 | 160 | 500 | 1000 | 2000 | 5000 |
“兵”字面朝上次数m | 14 | 38 | 52 | 66 | 78 | 88 | 280 | 550 | 1100 | 2750 |
“兵”字面朝上频率 |
|
|
|
|
|
|
|
|
|
|
下面有三个推断:![]() 投掷1000次时,“兵”字面朝上的次数是550,所以“兵”字面朝上的概率是
投掷1000次时,“兵”字面朝上的次数是550,所以“兵”字面朝上的概率是![]() ;
;![]() 随着实验次数的增加,“兵”字面朝上的频率总在
随着实验次数的增加,“兵”字面朝上的频率总在![]() 附近,显示出一定的稳定性,可以估计“兵”字面朝上的概率是
附近,显示出一定的稳定性,可以估计“兵”字面朝上的概率是![]() ;
;![]() 当实验次数为200次时,“兵”字面朝上的频率一定是
当实验次数为200次时,“兵”字面朝上的频率一定是![]() 其中合理的是
其中合理的是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()