Question

【题目】综合与探究：

已知二次函数y＝﹣x2+x+2的图象与x轴交于A，B两点（点B在点A的左侧），与y轴交于点C．

（1）求点A，B，C的坐标；

（2）求证：△ABC为直角三角形；

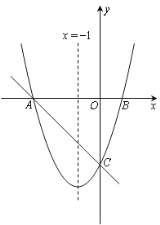
（3）如图，动点E，F同时从点A出发，其中点E以每秒2个单位长度的速度沿AB边向终点B运动，点F以每秒个单位长度的速度沿射线AC方向运动．当点F停止运动时，点E随之停止运动．设运动时间为t秒，连结EF，将△AEF沿EF翻折，使点A落在点D处，得到△DEF．当点F在AC上时，是否存在某一时刻t，使得△DCO≌△BCO？（点D不与点B重合）若存在，求出t的值；若不存在，请说明理由．

Answer 1

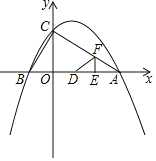
【答案】（1）点A的坐标为（4，0），点B的坐标为（﹣1，0），点C的坐标为（0，2）；（2）证明见解析；（3）t＝.

【解析】

（1）利用x=0和y=0解方程即可求出A、B、C三点坐标；
（2）先计算△ABC的三边长，根据勾股定理的逆定理可得结论；
（3）先证明△AEF∽△ACB，得∠AEF=∠ACB=90°，确定△AEF沿EF翻折后，点A落在x轴上点D处，根据△DCO≌△BCO时，BO=OD，列方程4-4t=1，可得结论．

（1）解：当y＝0时，﹣x+2＝0，

解得：x1＝1，x2＝4，

∴点A的坐标为（4，0），点B的坐标为（﹣1，0），

当x＝0时，y＝2，

∴点C的坐标为（0，2）；

（2）证明：∵A（4，0），B（﹣1，0），C（0，2），

∴OA＝4，OB＝1，OC＝2．

∴AB＝5，AC＝＝，

∴AC2+BC2＝25＝AB2，

∴△ABC为直角三角形；

（3）解：由（2）可知△ABC为直角三角形．且∠ACB＝90°，

∵AE＝2t，AF＝t，

∴，

又∵∠EAF＝∠CAB，

∴△AEF∽△ACB，

∴∠AEF＝∠ACB＝90°，

∴△AEF沿EF翻折后，点A落在x轴上点 D处，

由翻折知，DE＝AE，

∴AD＝2AE＝4t，

当△DCO≌△BCO时，BO＝OD，

∵OD＝4﹣4t，BO＝1，

∴4﹣4t＝1，t＝，

即：当t＝秒时，△DCO≌△BCO．