Question

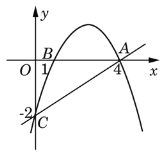
【题目】已知二次函数y=(x﹣m)(x﹣m﹣4)(m为常数)．

（1）求证：不论m为何值，该函数的图象与x轴总有两个不同的公共点；

（2）求证：不论m为何值，该函数的图象的顶点纵坐标不变；

（3）若该函数的图象与x轴交点为A、B，与y轴交点为C，当﹣3≤m≤﹣1时，△ABC面积S的取值范围为 ．

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）6≤S≤8．

【解析】

（1）当y=0时，(x-m)(x-m-4)=0，解得x1=m，x2=m+4，即可得到结论；

（2）图象与x轴的两个交点坐标为(m，0)、(m+4，0)，由抛物线的对称性可知图象顶点横坐标为m+2，代入解析式求得y=-4，从而求得结论；

（3）当-3≤m≤-1时，求出S=2|m2+4m|，然后根据二次函数的性质求解即可．

（1）当y=0时，(x-m)(x-m-4)=0，

解得：x1=m，x2=m+4，

∵m≠m+4，方程有两个不相等的实数根，

∴不论m为何值，函数图象与x轴总有两个不同的公共点；

（2）由（1）得图象与x轴的两个交点坐标为(m，0)、(m+4，0)，

由抛物线的对称性可知图象顶点横坐标为m+2，

把x=m+2代入y=(x﹣m)(x﹣m﹣4)得y=﹣4，

∴不论m为何值，该函数的图象的顶点纵坐标不变为﹣4；

（3）∵y=(x﹣m)(x﹣m﹣4)=x2﹣(2m+4)x+m2+4m，

∴C(0，m2+4m)．

∵图象与x轴的两个交点坐标为(m，0)、(m+4，0)，

∴AB=4，

∴SABOC×|m2+4m|=2|m2+4m|，

当m=﹣3时，S=2×3=6；当m=﹣1时，S=2×3=6，

当顶点在y轴上，即m=﹣2时，|m2+4m|最大值是4，故此时S=2×4=8，∴6≤S≤8．

故答案为：6≤S≤8．