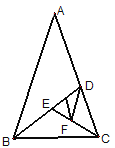
题目内容
【题目】在![]() 中,
中,![]() ,CD是AB边上的高,若
,CD是AB边上的高,若![]() .
.

(1)求CD的长.
(2)动点P在边AB上从点A出发向点B运动,速度为1个单位/秒;动点Q在边AC上从点A出发向点C运动,速度为v个单位秒![]() ,设运动的时间为
,设运动的时间为![]() ,当点Q到点C时,两个点都停止运动.
,当点Q到点C时,两个点都停止运动.
①若当![]() 时,
时,![]() ,求t的值.
,求t的值.
②若在运动过程中存在某一时刻,使![]() 成立,求v关于t的函数表达式,并写出自变量t的取值范围.
成立,求v关于t的函数表达式,并写出自变量t的取值范围.
【答案】(1)CD=8;(2)t=4;(3)![]() (
(![]() )
)
【解析】
(1)作AE⊥BC于E,根据等腰三角形三线合一的性质可得BE=![]() BC,然后利用勾股定理求出AE,再用等面积法可求出CD的长;
BC,然后利用勾股定理求出AE,再用等面积法可求出CD的长;
(2)①过B作BF⊥AC于F,易得BF=CD,分别讨论Q点在AF和FC之间时,根据△BQF≌△CPD,得到PD=QF,建立方程即可求出t的值;
(3)同(2)建立等式关系即可得出关系式,再根据Q在FC之间求出t的取值范围即可.
解:(1)如图,作AE⊥BC于E,

∵AB=AC,
∴BE=![]() BC=
BC=![]()
在Rt△ABE中,
![]()
∵△ABC的面积=![]()
∴![]()
(2)过B作BQ⊥AC,当Q在AF之间时,如图所示,

∵△ABC的面积=![]() ,AB=AC
,AB=AC
∴BF=CD
在Rt△CPD和Rt△BQF中
∵CP=BQ,CD=BF,
∴Rt△CPD≌Rt△BQF(HL)
∴PD=QF
在Rt△ACD中,CD=8,AC=AB=10
∴![]()
同理可得AF=6
∴PD=AD=AP=6-t,QF=AF-AQ=6-2t
由PD=QF得6-t=6-2t,解得t=0,
∵t>0,
∴此种情况不符合题意,舍去;
当Q点在FC之间时,如图所示,

此时PD=6-t,QF=2t-6
由PD=QF得6-t=2t-6,
解得t=4,
综上得t的值为4.
(3)同(2)可知v>1时,Q在AF之间不存在CP=BQ,Q在FC之间存在CP=BQ,Q在F点时,显然CP≠BQ,
∵运动时间为t,则AP=t,AQ=vt,
∴PD=6-t,QF=vt-6,
由PD=QF得6-t=vt-6,
整理得![]() ,
,
∵Q在FC之间,即AF<AQ≤AC
∴![]() ,代入
,代入![]() 得
得
![]() ,解得
,解得![]()
所以答案为![]() (
(![]() )
)

 阅读快车系列答案
阅读快车系列答案