题目内容
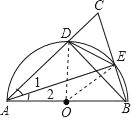
【题目】如图,AB是半圆O的直径,点C在半圆外,AC,BC与半圆交于D点和E点.
(1)请只用无刻度的直尺作出△ABC的两条高线,并写出作法;
(2)若AC=AB,连接DE,BE,求证:DE=BE.

【答案】见解析
【解析】【试题分析】(1)利用直径所对的圆周角是直角,直接连接BD、AE即可;(2)因为AB是⊙O的直径,根据直径所对的圆周角是直角得:∠AEB=90°,即AE⊥BC.
又AC=AB,根据“三线合一”得:∠1=∠2.连接OD,OE,根据同弧所对的圆周角是直角的一半得:∠DOE=∠BOE.根据在同圆中,相等的圆心角所对的弦也相等得:DE=BE.
【试题解析】
(1)如图所示:作法:连接AE与BD,则AE,BD是△ABC的两条高线;
(2)∵AB是⊙O的直径,
∴∠AEB=90°,即AE⊥BC.
又AC=AB,
∴∠1=∠2.
连接OD,OE,
∴∠DOE=∠BOE.
∴DE=BE.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目