��Ŀ����
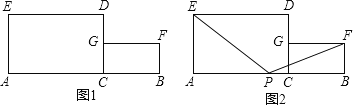
����Ŀ����ͼ����������A���ʾ����3��B���ʾ��b��C���ʾ��c����b.c����![]()
![]()
��1��b= ��c= ��
��2����ʹC.B����ľ�����A.B����ľ����2�������轫��C�����ƶ� ����λ���ȣ�
��3����A.B.C��ʼ���������˶�������A��ÿ��m����λ���ȵ��ٶ������˶���ͬʱ����B�͵�C�ֱ���ÿ��2����λ���Ⱥ�5����λ���ȵ��ٶ������˶������˶�ʱ��Ϊt�룻
�ٵ�A.B.C��ʾ�����ֱ��� . . ���ú�m.t�Ĵ���ʽ��ʾ����
������B���C֮��ľ����ʾΪd1����A���B֮��ľ����ʾΪd2����mΪ��ֵʱ��2d1��d2��ֵ��������ʱ��t�ı仯���ı䣬�������ʱ2d1��d2��ֵ��
���𰸡���1��b=-1��c=4��
(2) 1��9��
��3����-3-mt��-1+2t��4+5t����m=4��2d1��d2��ֵΪ12��
��������
��1����![]() ������ƽ��������ֵ�ķǸ��Կɵ�b+1=0��c-4=0���ݴ˿����b��c��ֵ��
������ƽ��������ֵ�ķǸ��Կɵ�b+1=0��c-4=0���ݴ˿����b��c��ֵ��
��
��2�������AB��BC�ij��ȣ�������ἴ�ɵó���C�����ƶ��ľ��룬�����⣻
��3���ٽ��·��=ʱ�����ٶ�д���𰸣�
�ڸ��ݢ��ȱ�ʾ��d1��d2���Ӷ���ʾ��2d1-d2��Ȼ�����2d1��d2��ֵ��������ʱ��t�ı仯���ı�ó�t��ϵ��Ϊ0���������m��ֵ���̶����2d1��d2��ֵ.
�⣺��1����![]()
��b+1=0��c-4=0
��b=-1��c=4
(2)�������֪��AB= 2��
��B C=4��
���C�����ƶ��������3��-5
���轫��C�����ƶ�1��9����λ��
�ʴ��ǣ�1��9��
��3���ٵ�A��ʾ������-3-mt����B��ʾ������-1+2t����C����ʾ������4+5t��
�ʴ��ǣ�-3-mt��-1+2t��4+5t��
�ڡߵ�A��ʾ������-3-mt����B��ʾ������-1+2t����C����ʾ������4+5��
��d1=4+5t-(-1+2t)=3t+5��d2=-1+2t-(-3-mt)=��m+2��t+2��
��2d1-d2=2��3t+5��-[��m+2��t+2]=��4-m��t+12��
��2d1��d2��ֵ��������ʱ��t�ı仯���ı�
��4-m=0��
��m=4��
�ʵ�m=4ʱ��2d1��d2��ֵ��������ʱ��t�ı仯���ı䣬��ʱ2d1��d2��ֵΪ12��

 ������״Ԫ���Ծ�ϵ�д�
������״Ԫ���Ծ�ϵ�д�����Ŀ��ij�̳�����![]() ��
��![]() ����Ʒ�Ƶ�ϴ�»������ۼ��ۼ����±���
����Ʒ�Ƶ�ϴ�»������ۼ��ۼ����±���
Ʒ�� |
|
|
���ۣ�Ԫ/̨�� | 1500 | 1800 |
�ۼۣ�Ԫ/̨�� | 1800 | 2200 |
��1�����̳�9�·���45000Ԫ����![]() ��
��![]() ����Ʒ�Ƶ�ϴ�»���ȫ����������9600Ԫ�����̳�9�·ݹ���
����Ʒ�Ƶ�ϴ�»���ȫ����������9600Ԫ�����̳�9�·ݹ���![]() ��
��![]() ����ϴ�»���������
����ϴ�»���������
��2�����̳�10�·��ֹ���![]() ��
��![]() ����Ʒ�Ƶ�ϴ�»�����ȥ36000Ԫ
����Ʒ�Ƶ�ϴ�»�����ȥ36000Ԫ
���ʸ��̳����м��ֽ�����������������з����г�����
��ͨ������˵��ϴ�»�ȫ������������ֽ�����������õ��������