Question

【题目】周末，小明从家步行去书店看书.出发小时后距家1.8千米时，爸爸驾车从家沿相同路线追赶小明，在地追上小明后，二人驾车继续前行到达书店.小明在书店看书，爸爸去单位地办事.如图是小明与爸爸两人之间距离（千米）与小明出发的时间（小时）之间的函数图象，（小明步行速度与爸爸驾车速度始终保持不变，彼此交流时间忽略不计），请根据图象回答下列问题：

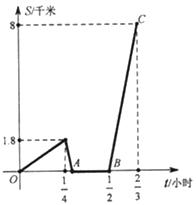
（1）小明步行速度是_____千米/小时，爸爸驾车速度是______千米/小时：

（2）图中点的坐标是______：

（3）求书店与家的路程；

（4）求爸爸出发多长时间，两人相距3千米.

Answer 1

【答案】（1）7.2，48；（2）；（3）12千米；（4）爸爸出发小时后，两人相距3千米

【解析】

（1）根据速度=距离÷时间即可求出小明和爸爸的速度；（2）设t小时爸爸追上小明，根据追上时距离相等列方程求出t值，进而可求出A点坐标；（3）根据爸爸出发到书店所用时间为（）小时，乘以爸爸的速度即可得答案；（4）由图象可知两人相距3千米时在图象线段BC上，设直线BC的解析式为S=kt+b，根据B、C两点坐标，利用待定系数法求出k、b的值，即可得BC的解析式，把S=3代入求出t的值，根据爸爸出发的时间等于t-即可得答案.

（1）小明步行速度为：1.8÷=7.2(千米/小时)，

爸爸驾车速度为：8÷（）=48(千米/小时)，

故答案为：7.2，48

（2）设t小时爸爸追上小明，

∴48t=7.2t+1.8，

解得：t=，

∴tA=+=，

∴A点坐标为（，0），

故答案为：（，0）

（3）爸爸出发到书店所用时间为（）小时，

∴书店与家的路程为：48×（）=12（千米），

答：书店与家的路程为12千米.

（4）由图象可知两人相距3千米时在图象线段BC上，设直线BC的解析式为S=kt+b，

∵B（，0），C（，8），

∴，

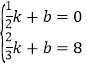解得：，

∴BC的解析式为S=48t-24，

当S=3时，3=48t-24，

解得：t=，

∵爸爸从小时出发，

∴-=（小时），

答：爸爸出发小时，两人相距3千米.