题目内容
【题目】如图,抛物线经过A(![]() ,0),B(
,0),B(![]() ,0),C(0,2)三点.
,0),C(0,2)三点.
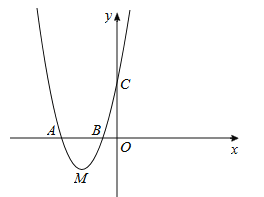
(1)求抛物线的解析式;
(2)在直线AC下方的抛物线上有一点D,使得△DCA的面积最大,求点D的坐标;
(3)设点M是抛物线的顶点,试判断抛物线上是否存在点H满足![]() ?若存在,请求出点H的坐标;若不存在,请说明理由.
?若存在,请求出点H的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)D(-1,-1);(3)(
;(2)D(-1,-1);(3)(![]() ,
,![]() ).
).
【解析】
试题分析:(1)根据待定系数法,可得抛物线的解析式;
(2)根据图形的割补法,可得面积的和差,根据二次函数的性质,可得答案;
(3)根据余角的性质,可得∠AMN=∠NKM,根据相似三角形的判定与性质,可得![]() ,根据解方程组,可得H点坐标.
,根据解方程组,可得H点坐标.
试题解析:(1)设抛物线的解析式为![]() ,将A(﹣2,0),B(
,将A(﹣2,0),B(![]() ,0)代入解析式,得:
,0)代入解析式,得: ,解得:
,解得:![]() .∴抛物线的解析式是
.∴抛物线的解析式是![]() ;
;
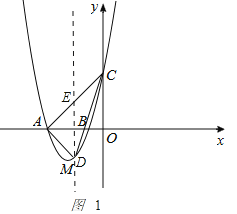
(2)由题意可求得AC的解析式为![]() ,如图1,设D点的坐标为(t,
,如图1,设D点的坐标为(t,![]() ),过D作DE⊥x轴交AC于E点,∴E点的坐标为(t,t+2),DE=
),过D作DE⊥x轴交AC于E点,∴E点的坐标为(t,t+2),DE=![]()
![]() ,用h表示点C到线段DE所在直线的距离,
,用h表示点C到线段DE所在直线的距离,
![]() =
=![]() ,∵﹣2<t<0,
,∵﹣2<t<0,
∴当t=﹣1时,△DCA的面积最大,此时D点的坐标为(﹣1,﹣1);
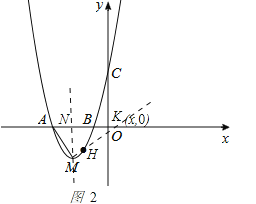
(3)存在点H满足∠AMH=90°,由(1)知M点的坐标为(![]() ,
,![]() ),如图2:作MH⊥AM交x轴于点K(x,0),作MN⊥x轴于点N,∵∠AMN+∠KMA=90°,∠NKM+∠KMN=90°,∴∠AMN=∠NKM.∵∠ANM=∠MNK,∴△AMN∽△MKN,∴
),如图2:作MH⊥AM交x轴于点K(x,0),作MN⊥x轴于点N,∵∠AMN+∠KMA=90°,∠NKM+∠KMN=90°,∴∠AMN=∠NKM.∵∠ANM=∠MNK,∴△AMN∽△MKN,∴![]() ,∴
,∴![]() =ANNK,∴
=ANNK,∴![]() ,解得
,解得![]() ,∴K点坐标为(
,∴K点坐标为(![]() ,0),∴直线MK的解析式为
,0),∴直线MK的解析式为![]() ,∴
,∴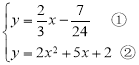 ,把①代入②,化简得
,把①代入②,化简得![]() .△=
.△=![]() ﹣4×48×55=64×4=256>0,∴
﹣4×48×55=64×4=256>0,∴![]() ,
,![]() ,将
,将![]() 代入
代入![]() ,解得
,解得![]() ,∴直线MN与抛物线有两个交点M、H,∴抛物线上存在点H,满足∠AMH=90°,此时点H的坐标为(
,∴直线MN与抛物线有两个交点M、H,∴抛物线上存在点H,满足∠AMH=90°,此时点H的坐标为(![]() ,
,![]() ).
).

 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案【题目】某商场销售![]() 、
、![]() 两种品牌的洗衣机,进价及售价如下表:
两种品牌的洗衣机,进价及售价如下表:
品牌 |
|
|
进价(元/台) | 1500 | 1800 |
售价(元/台) | 1800 | 2200 |
(1)该商场9月份用45000元购进![]() 、
、![]() 两种品牌的洗衣机,全部售完后获利9600元,求商场9月份购进
两种品牌的洗衣机,全部售完后获利9600元,求商场9月份购进![]() 、
、![]() 两种洗衣机的数量;
两种洗衣机的数量;
(2)该商场10月份又购进![]() 、
、![]() 两种品牌的洗衣机共用去36000元
两种品牌的洗衣机共用去36000元
①问该商场共有几种进货方案?请你把所有方案列出来;
②通过计算说明洗衣机全部销售完后哪种进货方案所获得的利润最大

