题目内容
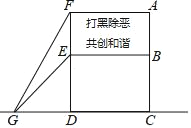
【题目】2018年年初,某小区应辖区派出所要求在广场树立一个“打黑除恶,共创和谐”的矩形电子灯牌,如图所示,施工人员在两侧加固合金框架,已知合金框架底端G距广告牌立柱距离FD为4米,从G点测得广告牌顶端F点和底端E点的仰角分别是60°和45°.
(1)若AF长为5米,求灯牌的面积;
(2)求两侧加固的铝合金框架总共用料多少米?(本题中的计算过程和结果均保留根号)
【答案】(1)灯牌的面积为(20![]() ﹣20)平方米;(2)(16+8
﹣20)平方米;(2)(16+8![]() )米.
)米.
【解析】分析:(1)在Rt△GDF中,利用DF=GDtan∠FGD求得DF的长,在Rt△DEG中由∠EGD=45°知GD=ED=4,根据EF=DF-DE,进一步求解可得;
(2)根据FG=![]() 、GE=
、GE=![]() 分别求得FG、GE的长,继而可得答案.
分别求得FG、GE的长,继而可得答案.
详解:(1)在Rt△GDF中,∵∠FGD=60°、GD=4,
∴DF=GDtan∠FGD=4![]() ,
,
在Rt△DEG中,∵∠EGD=45°,
∴GD=ED=4,
∴EF=DF﹣DE=4![]() ﹣4,
﹣4,
∴S矩形=5(4![]() ﹣4)=20
﹣4)=20![]() ﹣20(平方米),
﹣20(平方米),
答:灯牌的面积为(20![]() ﹣20)平方米;
﹣20)平方米;
(2)在Rt△GDF中,FG=![]() =8,
=8,
在Rt△DEG中,GE=![]() =4
=4![]() ,
,
因此两侧加固的铝合金框架总共用料2(8+4![]() )=(16+8
)=(16+8![]() )米.
)米.

练习册系列答案
相关题目





