题目内容
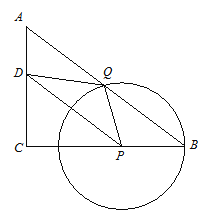
【题目】如图,在Rt![]() ABC中,∠C=90
ABC中,∠C=90![]() ,AC=8,BC=6,
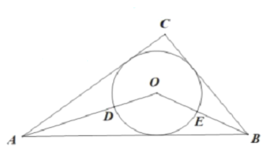
,AC=8,BC=6,![]() O为ABC的内切圆,OA,OB与
O为ABC的内切圆,OA,OB与![]() O分别交于点D,E,则劣弧DE的长是________.
O分别交于点D,E,则劣弧DE的长是________.
【答案】![]()
【解析】
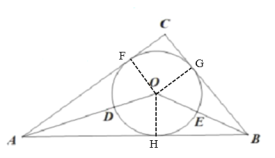
作OF⊥AC于点F,OG⊥BC于点G,OH⊥AB于点H,得到四边形CFOG是矩形,根据切线长定理得到圆O的半径,再根据角平分线得到劣弧DE所对的圆心角,最后根据弧长的计算公式即可解答.
解:如图,作OF⊥AC于点F,OG⊥BC于点G,OH⊥AB于点H,
设圆O的半径为r,
则四边形CFOG是矩形,
在Rt△ABC中,∵∠C=90![]() ,AC=8,BC=6,
,AC=8,BC=6,
∴AB=![]() ,
,
∵![]() O为ABC的内切圆,
O为ABC的内切圆,
∴OF=OG,
∴矩形CFOG是正方形,
∴CF=CG=r,
则AF=AH=8-r,BG=BH=6-r,
∴AH+BH=8-r+6-r=10,解得:r=2,
又∵![]() O为ABC的内切圆,
O为ABC的内切圆,
∴OA,OB分别平分∠CAB、∠ABC,
∴∠OAB=![]() ∠CAB,∠OBA=
∠CAB,∠OBA=![]() ∠ABC,
∠ABC,
∵∠C=90°,
∴∠OAB+∠OBA=![]() (∠CAB+∠ABC)=
(∠CAB+∠ABC)=![]() ×90°=45°,
×90°=45°,
∴∠DOE=180°-(∠OAB+∠OBA)=135°,
∴劣弧DE的长是:![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目