题目内容
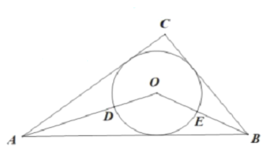
【题目】如图所示,在△ABC中,AB=AC=![]() ,∠B=30°,点O为边BC上一点以O为圆心的圆经过点A,B.
,∠B=30°,点O为边BC上一点以O为圆心的圆经过点A,B.
(1)求作圆O(尺规作图,保留作留痕迹,不写作法);
(2)求证:AC是OO的切线;
(3)若点P为圆O上一点,且弧PA=弧PB,连接PC,求线段PC的长.
【答案】(1)如图所示即为答案;(2)详见解析;(3)![]() 或2
或2![]()
【解析】
(1)根据外心的定义即可求作圆O;
(2)根据切线的判定即可证明AC是⊙O的切线;
(3)根据点P为圆O上一点,且弧PA=弧PB,连接PC,即可求线段PC的长.
解:(1)如图,圆O即为所求;
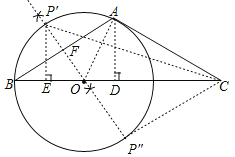
(2)证明:连接OA,
∵OA=OB,
∴∠OAB=∠B=30°,
∵AB=AC,
∴∠ACB=∠B=30°,
∴∠BAC=120°,
∴∠CAO=∠BAC﹣∠OAB=90°,
∴OA⊥AC,OA是⊙O的半径,
∴AC是⊙O的切线;
(3)∵弧PA=弧PB,
∴符合条件的点P有两个,P′和P″,连接P′C和P″C,
作P′E⊥BC于点E,
∵OP′⊥AB,
根据垂径定理,得
AF=BF=![]() AB=
AB=![]() ,
,
∵∠B=30,
∴∠P′OB=60°,
∴OB=![]() ,
,
∴P′E=BF=![]() ,
,
BE=![]() OB=
OB=![]() ,
,
∵AB=AC=2![]() ,
,
作AD⊥BC于点D,则AD=![]() ,DC=
,DC=![]() ,
,
∴BC=2DC=2![]() ,
,
∴CE=BC﹣BE=![]() ,
,
∴P′C=![]() ;
;
连接P″C,
∵OA=OP″,∠AOC=∠COP″=60°,OC=OC,
∴△AOC≌△P″OC(SAS),
∴P″C=AC=2![]() .
.
综上所述:线段PC的长为![]() 或2
或2![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目