题目内容
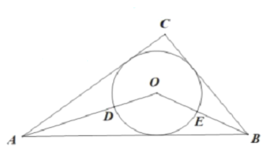
【题目】已知:如图,圆O是△ABC的外接圆,AO平分∠BAC.
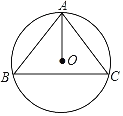
(1)求证:△ABC是等腰三角形;
(2)当OA=4,AB=6,求边BC的长.
【答案】(1)见解析;(2)3![]()
【解析】
(1)连接OB、OC,先证明∠OBA=∠OCA=∠BAO=∠CAO,再证明△OAB≌△OAC得AB=AC,问题得证;
(2)延长AO交BC于点H,先证明AH⊥BC,BH=CH,设OH=b,BH=CH=a,根据OA=4,AB=6,由勾股定理列出a、b的方程组,解得a、b,便可得BC.
解:(1)连接OB、OC,
∵OA=OB=OC,OA平分∠BAC,
∴∠OBA=∠OCA=∠BAO=∠CAO,
在△OAB和△OAC中,
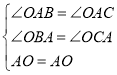 ,
,
∴△OAB≌△OAC(AAS),
∴AB=AC
即△ABC是等腰三角形;
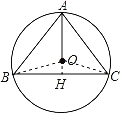
(2)延长AO交BC于点H,
∵AH平分∠BAC,AB=AC,
∴AH⊥BC,BH=CH,
设OH=b,BH=CH=a,
∵BH2+OH2=OB2, OA=4,AB=6,
则 ![]() ①
①
![]() BH2+AH2=AB2,OA=4,AB=6,
BH2+AH2=AB2,OA=4,AB=6,
则![]() ②
②
②-①得:![]()
![]()
把![]() 代入①得:
代入①得:![]() (舍)
(舍)
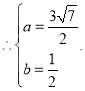
∴BC=2a=3![]() .
.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目