题目内容
【题目】如图,BC是路边坡角为30°,长为10米的一道斜坡,在坡顶灯杆CD的顶端D处有一探射灯,射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN和∠DBN分别是37°和60°(图中的点A、B、C、D、M、N均在同一平面内,CM∥AN).
(1)求灯杆CD的高度;
(2)求AB的长度(结果精确到0.1米).(参考数据:![]() =1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)
=1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)

【答案】(1)10米;(2)11.4米
【解析】
(1)延长DC交AN于H.只要证明BC=CD即可;
(2)在Rt△BCH中,求出BH、CH,在 Rt△ADH中求出AH即可解决问题.
(1)如图,延长DC交AN于H,
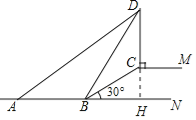
∵∠DBH=60°,∠DHB=90°,
∴∠BDH=30°,
∵∠CBH=30°,
∴∠CBD=∠BDC=30°,
∴BC=CD=10(米);
(2)在Rt△BCH中,CH=![]() BC=5,BH=5
BC=5,BH=5![]() ≈8.65,
≈8.65,
∴DH=15,
在Rt△ADH中,AH=![]() ≈
≈![]() =20,
=20,
∴AB=AH﹣BH=20﹣8.65=11.4(米).

练习册系列答案
相关题目
【题目】某公司欲招聘一名公务人员,对甲、乙两位应试者进行了面试和笔试,他们的成绩(百分制)如表所示:
应试者 | 面试 | 笔试 |
甲 | 86 | 90 |
乙 | 92 | 83 |
(1)如果公司认为面试和笔试同等重要,从他们的成绩看,谁将被录取?
(2)如果公司认为作为公务人员面试成绩应该比笔试成绩更重要,并分别赋予它们6和4的权,计算甲、乙两人各自的平均成绩,谁将被录取?