Question

【题目】如图，已知二次函数的图像与x轴交于A、B两点(点A在点B左侧)，与y轴交于点C.

(1)求线段BC的长；

(2)当0≤y≤3时，请直接写出x的范围；

(3)点P是抛物线上位于第一象限的一个动点，连接CP，当∠BCP＝90o时，求点P的坐标.

Answer 1

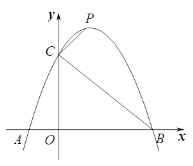
【答案】（1）5 ；（2），；（3）点P坐标为(，).

【解析】

（1）分别求出点B和点C的坐标，再运用勾股定理即可求出BC的长；

（2）求出y=0和y=3时相应的x的值，结合函数的图象即可得到答案；

（3）过点P作PD⊥y轴，设点P坐标为(x, )，则点D坐标为(0, )，表示出PD，CD，证明△PDC∽△COB，得出，列方程求解即可.

(1)当x＝0时，y＝3，

∴C(0,3)，

∴OC＝3

当y＝0时，解得x1＝－1，x2＝4

∴A(－1,0)，B(4,0)，

∴OA＝1，OB＝4

在Rt△BOC中，BC＝＝5；

(2) 当y＝0时，解得x1＝－1，x2＝4

当y＝3时，解得x1＝0，x2＝4

∴当0≤y≤3时，，

(3)过点P作PD⊥y轴

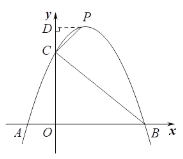
设点P坐标为(x, )，则点D坐标为(0, )

∴PD＝x，CD＝－3＝/p>

∵∠BCP＝90°，

∴∠PCD＋∠BCO＝90°，

∵∠PCD＋∠CPD＝90°，

∴∠BCO＝∠CPD

∵∠PDC＝∠BOC＝90°，

∴△PDC∽△COB

∴，

∴，

∴x＝或x＝0(舍去)

当x＝时，y＝

∴点P坐标为(，).